Función de Transferencia: Descubre cómo entenderla y utilizarla de manera efectiva

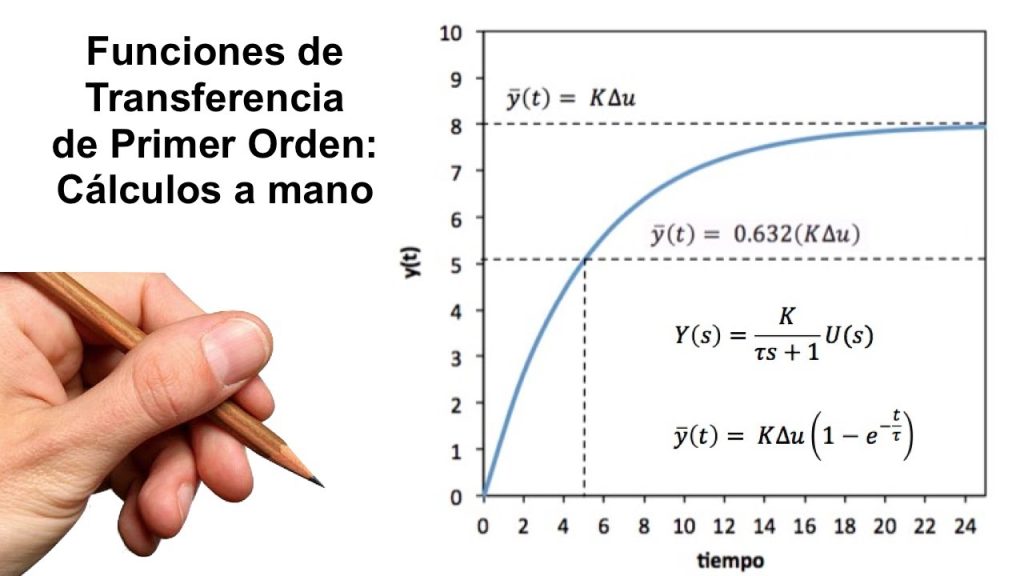
La función de transferencia es un concepto fundamental en ingeniería y en el análisis de sistemas dinámicos. Se utiliza para describir la relación entre la entrada y la salida de un sistema, y permite comprender cómo un sistema responde a diferentes señales de entrada. La función de transferencia se aplica en una amplia variedad de campos, como la electrónica, la mecánica, la robótica y el control de procesos.

Exploraremos qué es exactamente una función de transferencia, cómo se representa matemáticamente y cómo se puede utilizar para analizar y diseñar sistemas. También discutiremos algunas propiedades importantes de las funciones de transferencia y cómo se pueden manipular algebraicamente. Comprender la función de transferencia es fundamental para aquellos que trabajan en el campo del control y la automatización, ya que permite desarrollar estrategias efectivas para mejorar la respuesta y el rendimiento de los sistemas. ¡Vamos a sumergirnos en el mundo de las funciones de transferencia!

Qué es una función de transferencia y para qué se utiliza en ingeniería

En el campo de la ingeniería, especialmente en disciplinas como la electrónica y la control automático, la función de transferencia es una herramienta fundamental para comprender y analizar sistemas dinámicos. Una función de transferencia es una representación matemática que relaciona la entrada y la salida de un sistema. Proporciona información sobre cómo un sistema responde a diferentes entradas y cómo se comporta en términos de frecuencia.

La función de transferencia se basa en la transformada de Laplace, una técnica matemática utilizada para analizar señales y sistemas lineales e invariantes en el tiempo. La transformada de Laplace permite representar una señal en el dominio del tiempo como una función compleja en el dominio de la frecuencia. Esta representación en el dominio de la frecuencia facilita el análisis y diseño de sistemas.

En pocas palabras, una función de transferencia describe la relación entre la entrada y la salida de un sistema en términos de ganancia y fase en diferentes frecuencias. Especifica cómo las diferentes frecuencias de entrada se transmiten o se atenúan en la salida del sistema. Esto es especialmente útil cuando se trabaja con señales de entrada que varían en el tiempo, como las señales senoidales utilizadas frecuentemente en aplicaciones de control.

Cómo entender una función de transferencia

Para comprender una función de transferencia, es importante familiarizarse con su estructura y cómo se representa. La forma general de una función de transferencia es:

H(s) = N(s) / D(s)

Donde H(s) representa la función de transferencia en términos de la variable compleja s, N(s) es el numerador de la función de transferencia y D(s) es el denominador. Los polinomios N(s) y D(s) están compuestos por coeficientes y potencias de s.

La variable compleja s en una función de transferencia representa la frecuencia en el dominio de Laplace. Puede ser imaginaria, real o compleja y está relacionada con la frecuencia angular ω a través de la fórmula s = jω. Aquí, j es la unidad imaginaria √(-1).

La función de transferencia puede tener diferentes órdenes, que se refieren al grado más alto del polinomio del denominador D(s). Por ejemplo, una función de transferencia de primer orden tendría un denominador de la forma s + a, donde a es una constante. Una función de transferencia de segundo orden tendría un denominador de la forma s^2 + bs + c.

Utilidad práctica de las funciones de transferencia

Las funciones de transferencia son muy útiles en ingeniería porque facilitan el análisis y diseño de sistemas. Al comprender la función de transferencia de un sistema, es posible predecir y controlar su comportamiento en respuesta a diferentes entradas. Esto es especialmente importante en aplicaciones de control automático, donde se utilizan para diseñar controladores que aseguren la estabilidad y rendimiento deseado del sistema.

La función de transferencia también permite realizar análisis de estabilidad y respuesta en frecuencia. El diagrama de Bode, por ejemplo, es una representación gráfica que muestra cómo la ganancia y la fase de una función de transferencia varían con la frecuencia. Esto permite identificar las frecuencias en las que el sistema puede presentar problemas como oscilaciones o inestabilidad. Además, la función de transferencia puede utilizarse para realizar simulaciones y tomar decisiones basadas en resultados numéricos antes de implementar un sistema en la práctica.

Una función de transferencia es una herramienta fundamental en ingeniería que permite analizar y entender sistemas dinámicos. Proporciona información sobre cómo los sistemas responden a diferentes entradas en términos de ganancia y fase en diferentes frecuencias. Al comprender las funciones de transferencia, los ingenieros pueden diseñar y optimizar sistemas para lograr el rendimiento deseado.

Cuál es la importancia de entender y utilizar funciones de transferencia de manera efectiva

Las funciones de transferencia son herramientas fundamentales en el campo de la ingeniería y las ciencias aplicadas. Estas funciones representan la relación entre la entrada y la salida de un sistema, proporcionando información clave sobre su comportamiento y características.

Es crucial entender y utilizar estas funciones de transferencia de manera efectiva, ya que nos permiten analizar y diseñar sistemas de forma precisa y eficiente. Al comprender cómo funciona un sistema y cómo se relaciona con su entrada y salida, podemos realizar ajustes y mejoras para optimizar su desempeño.

Análisis de sistemas mediante funciones de transferencia

Una de las principales ventajas de utilizar funciones de transferencia es su capacidad para analizar sistemas complejos de manera sencilla. Estas funciones simplifican la representación matemática de un sistema, lo cual facilita su estudio y comprensión.

Para realizar el análisis de un sistema utilizando funciones de transferencia, es necesario plantear el problema en términos de variables de entrada y salida. A partir de ahí, se pueden establecer las ecuaciones diferenciales que describen el comportamiento del sistema.

Una vez obtenidas las ecuaciones diferenciales, se puede aplicar la transformada de Laplace para obtener la función de transferencia. Esta función relaciona la transformada de Laplace de la salida con la transformada de Laplace de la entrada, y resume el comportamiento del sistema en una única expresión matemática.

Aplicación en el diseño de controladores

Otra aplicación fundamental de las funciones de transferencia es en el diseño de sistemas de control. Estas funciones nos permiten modelar y simular el comportamiento de un sistema, lo cual es esencial para desarrollar estrategias de control efectivas.

Al diseñar un controlador para un sistema determinado, es necesario conocer la función de transferencia del sistema. Esta información nos permite analizar su respuesta ante diferentes entradas y establecer los parámetros óptimos del controlador.

Además, las funciones de transferencia también nos permiten simular el comportamiento del sistema en diferentes escenarios, lo cual es útil para evaluar el desempeño del controlador antes de implementarlo en la práctica.

Entender y utilizar de manera efectiva las funciones de transferencia es fundamental para el análisis y diseño de sistemas. Estas funciones nos brindan una representación matemática simplificada del sistema, lo cual facilita su estudio y comprensión.

Además, las funciones de transferencia son clave en el diseño de sistemas de control, ya que nos permiten modelar y simular el comportamiento del sistema para desarrollar estrategias de control efectivas.

Por lo tanto, al dominar el concepto de funciones de transferencia y saber cómo utilizarlas correctamente, podremos optimizar el desempeño de los sistemas y lograr resultados más precisos y eficientes en nuestras aplicaciones de ingeniería y ciencias aplicadas.

Cuáles son los elementos básicos de una función de transferencia y cómo se representan

La función de transferencia es una herramienta fundamental en el análisis y diseño de sistemas dinámicos. Se utiliza para describir la relación entre la entrada y la salida de un sistema en términos de variables de dominio de frecuencia. Para comprender cómo funciona una función de transferencia, es importante conocer los elementos básicos que la componen.

Numerador y denominador

En su forma más sencilla, una función de transferencia se puede representar mediante dos polinomios: el numerador y el denominador. El numerador representa la salida del sistema y el denominador representa la entrada del sistema. Estos polinomios están compuestos por coeficientes y potencias de la variable compleja "s". La variable "s" se utiliza para denotar la frecuencia compleja, que combina tanto la parte imaginaria (representando la componente sinusoidal) como la real (representando la componente exponencial).

El numerador y denominador se pueden expresar utilizando la siguiente notación:

num(s) = a_ns^n + a_(n-1)s^(n-1) + ... + a_1s + a_0
den(s) = b_ms^m + b_(m-1)s^(m-1) + ... + b_1s + b_0

Donde "a_n" y "b_m" son los coeficientes de los respectivos polinomios y "n" y "m" son las potencias más altas de "s" en el numerador y denominador, respectivamente.

Polos y ceros

Los polos y ceros de una función de transferencia son puntos en el plano complejo que representan las singularidades del sistema. Los ceros corresponden a los valores de "s" para los cuales el numerador es igual a cero, mientras que los polos corresponden a los valores de "s" para los cuales el denominador es igual a cero.

La ubicación de los polos y ceros en el plano complejo tiene un gran impacto en el comportamiento del sistema. Los polos determinan la estabilidad del sistema y su respuesta transitoria, mientras que los ceros influyen en la cancelación de frecuencias y la respuesta en frecuencia del sistema.

Rango de frecuencias

El rango de frecuencias en el cual una función de transferencia es válida también es un aspecto importante a tener en cuenta. Algunas funciones de transferencia pueden ser adecuadas solo para frecuencias bajas, mientras que otras pueden funcionar bien en un amplio rango de frecuencias. Esto depende de los componentes y la estructura del sistema subyacente.

Es importante tener en cuenta que la función de transferencia es una representación matemática idealizada del comportamiento real del sistema. Siempre existe cierta discrepancia entre la teoría y la práctica, por lo que es necesario realizar ajustes y considerar las limitaciones del sistema real durante la implementación.

Comprender los elementos básicos de una función de transferencia, como el numerador, el denominador, los polos y los ceros, así como el rango de frecuencias válido, es fundamental para entender y utilizar eficazmente esta herramienta en el análisis y diseño de sistemas dinámicos.

Cuál es la diferencia entre una función de transferencia de sistemas lineales y no lineales

Para comprender la diferencia entre una función de transferencia de sistemas lineales y no lineales, es importante tener claros los conceptos básicos de ambos tipos de sistemas.

Sistemas lineales:

Un sistema lineal se caracteriza por cumplir con el principio de superposición, lo que significa que si se aplica una entrada a un sistema, obtenemos una salida proporcional a dicha entrada. En términos matemáticos, esto se representa mediante una ecuación lineal.

• En un sistema lineal, la función de transferencia es una relación entre la salida y la entrada en el dominio de la frecuencia.
• La función de transferencia de un sistema lineal puede expresarse en forma algebraica utilizando la transformada de Laplace.
• Las funciones de transferencia lineales son más fáciles de entender y manipular matemáticamente.

Sistemas no lineales:

Por otro lado, un sistema no lineal no cumple con el principio de superposición. Es decir, la salida del sistema no es proporcional a la entrada. Esto implica que la relación entre entrada y salida no puede ser representada mediante una ecuación lineal.

• En un sistema no lineal, la función de transferencia no puede ser expresada en forma algebraica utilizando la transformada de Laplace.
• Las funciones de transferencia no lineales pueden tener comportamientos complejos y difíciles de predecir o analizar matemáticamente.
• Estos sistemas pueden presentar fenómenos como distorsión armónica, saturación y otros efectos no presentes en sistemas lineales.

La diferencia fundamental entre una función de transferencia de sistemas lineales y no lineales radica en la posibilidad de representar la relación entrada-salida mediante una ecuación lineal. Mientras que los sistemas lineales son más fáciles de analizar y predecir matemáticamente, los sistemas no lineales presentan comportamientos más complejos y pueden tener efectos no deseados como distorsiones o saturaciones.

Cómo se calcula y interpreta la respuesta en frecuencia de una función de transferencia

La respuesta en frecuencia de una función de transferencia es una herramienta fundamental en la ingeniería de sistemas y en el análisis de circuitos electrónicos. Permite comprender cómo reacciona un sistema a diferentes frecuencias de entrada y cómo se atenúan o amplifican las señales en función de su frecuencia.

Para calcular la respuesta en frecuencia de una función de transferencia, es necesario realizar un análisis de Fourier. Este análisis descompone la señal de entrada en sus componentes de frecuencia, permitiendo evaluar cómo afecta cada componente al sistema. El resultado del análisis de Fourier es la representación de la función de transferencia en el dominio de la frecuencia.

La respuesta en frecuencia se interpreta mediante diagramas de Bode, que muestran la magnitud y la fase de la función de transferencia en función de la frecuencia. En el diagrama de magnitud, se representa la ganancia del sistema en decibelios, mientras que en el diagrama de fase se muestra el desfase de la señal de salida con respecto a la señal de entrada. Ambos diagramas son fundamentales para comprender el comportamiento de un sistema en diferentes frecuencias.

En el diagrama de magnitud, es común observar picos y valles que indican las frecuencias resonantes del sistema. Un pico indica una amplificación en esa frecuencia, mientras que un valle indica una atenuación. Estos picos y valles están directamente relacionados con los polos y ceros de la función de transferencia. Los polos representan las frecuencias donde la amplitud de la respuesta en frecuencia es máxima, mientras que los ceros indican las frecuencias donde la amplitud es mínima.

El diagrama de fase, por su parte, muestra cómo se desfasa la señal de salida con respecto a la señal de entrada en función de la frecuencia. Permite identificar si la respuesta del sistema es retardada o adelantada respecto a la señal de entrada. Además, los cambios bruscos de fase indican la presencia de polos y ceros en la función de transferencia.

La interpretación de la respuesta en frecuencia es crucial para el diseño y análisis de sistemas y circuitos electrónicos. Permite predecir cómo se comportará un sistema ante diferentes frecuencias de entrada y determinar su estabilidad y robustez. Además, facilita la selección de componentes y ajuste de parámetros para obtener la respuesta deseada.

Entender y utilizar de manera efectiva la respuesta en frecuencia de una función de transferencia es fundamental para el análisis y diseño de sistemas y circuitos electrónicos. Mediante el cálculo y la interpretación de dicha respuesta, es posible comprender cómo afecta cada componente de frecuencia al sistema y determinar su comportamiento en diferentes frecuencias de entrada.

Cuáles son las principales técnicas para simplificar y analizar funciones de transferencia complejas

1. Descomposición en fracciones parciales

Una de las técnicas más utilizadas para simplificar una función de transferencia compleja es la descomposición en fracciones parciales. Esta técnica se utiliza cuando la función de transferencia contiene términos polinomiales en su denominador.

La descomposición en fracciones parciales consiste en descomponer la función de transferencia en una suma de fracciones racionales simples, donde cada fracción tiene un denominador lineal (es decir, un polinomio de grado 1). Para ello, se deben identificar los factores irreducibles del denominador y determinar los coeficientes correspondientes en cada fracción parcial.

Una vez descompuesta la función de transferencia en fracciones parciales, podemos analizar cada una de ellas por separado, lo que nos permite obtener información más detallada acerca del comportamiento del sistema.

2. Series de Taylor

Otra técnica útil para analizar funciones de transferencia complejas es la aproximación mediante series de Taylor. Esta técnica se basa en la idea de que cualquier función analítica puede ser representada como una serie infinita de términos.

En el caso de las funciones de transferencia, podemos utilizar la serie de Taylor para aproximar la función alrededor de un punto específico. Esto nos permite obtener una aproximación lineal o cuadrática de la función en ese punto, lo cual puede ser de gran utilidad para entender su comportamiento local.

La aproximación mediante series de Taylor también nos permite obtener derivadas de la función de transferencia en ese punto, lo que puede ser útil para analizar su estabilidad y respuesta en el dominio del tiempo.

3. Transformada de Laplace inversa

En algunos casos, la función de transferencia puede ser muy compleja y difícil de analizar directamente. En estos casos, una técnica útil es utilizar la transformada de Laplace inversa para obtener la respuesta temporal del sistema.

La transformada de Laplace inversa nos permite obtener la función en el dominio del tiempo a partir de su representación en el dominio de la frecuencia. Para ello, utilizamos tablas de transformadas o técnicas algebraicas para invertir la expresión en el dominio de la frecuencia.

Una vez obtenida la función en el dominio del tiempo, podemos analizar su comportamiento utilizando técnicas de análisis de señales, como por ejemplo, determinando su respuesta al impulso, su respuesta al escalón o su respuesta en frecuencia.

4. Análisis gráfico

Además de las técnicas matemáticas, el análisis gráfico también puede ser de gran ayuda para entender y simplificar funciones de transferencia complejas. El uso de gráficos nos permite visualizar de forma intuitiva el comportamiento del sistema.

Podemos trazar diagramas de Bode para analizar la respuesta en frecuencia de la función de transferencia, o diagramas de Nyquist para analizar la estabilidad del sistema. También podemos utilizar diagramas de polos y ceros para visualizar los puntos críticos de la función y su influencia en el comportamiento del sistema.

El análisis gráfico puede ser especialmente útil cuando se trabaja con sistemas de mayor complejidad, ya que nos permite obtener una visión general y detectar posibles problemas o mejoras en el diseño del sistema.

Existen diversas técnicas para simplificar y analizar funciones de transferencia complejas. La descomposición en fracciones parciales, las series de Taylor, la transformada de Laplace inversa y el análisis gráfico son herramientas fundamentales en este proceso. Al utilizar estas técnicas de manera efectiva, podemos entender el comportamiento de los sistemas y tomar decisiones informadas para optimizar su funcionamiento.

Cómo se utilizan las funciones de transferencia en el diseño de controladores de sistemas

Las funciones de transferencia son herramientas fundamentales en el diseño de controladores de sistemas. Estas funciones nos permiten comprender y analizar cómo se comportan los sistemas dinámicos en respuesta a estímulos externos. En este artículo, exploraremos en detalle qué son las funciones de transferencia y cómo se utilizan de manera efectiva en el diseño de controladores.

¿Qué es una función de transferencia?

Una función de transferencia es una representación matemática que describe la relación entre la señal de entrada y la señal de salida de un sistema dinámico. Se utiliza para modelar sistemas reales como circuitos eléctricos, sistemas térmicos, sistemas mecánicos, entre otros. La función de transferencia se define mediante una ecuación algebraica que relaciona la transformada de Laplace de la salida con la transformada de Laplace de la entrada.

La función de transferencia es una herramienta poderosa que nos permite estudiar el comportamiento de un sistema sin necesidad de conocer los detalles internos del mismo. A través de la función de transferencia, podemos analizar la estabilidad del sistema, su respuesta en frecuencia, su respuesta transitoria, entre otras características importantes.

Utilizando funciones de transferencia en el diseño de controladores

Una de las aplicaciones más comunes de las funciones de transferencia es en el diseño de controladores. Un controlador es un dispositivo o algoritmo que ajusta la señal de entrada de un sistema con el objetivo de lograr un comportamiento deseado en la salida. El diseño de un controlador efectivo requiere un profundo análisis y comprensión del sistema a controlar. Aquí es donde entran en juego las funciones de transferencia.

En el diseño de controladores, utilizamos la función de transferencia del sistema a controlar para determinar las características del controlador. A través del análisis de la función de transferencia, podemos identificar las frecuencias críticas, las singularidades y los polos del sistema. Estos parámetros son fundamentales para seleccionar la estructura y los parámetros del controlador adecuados.

Además, las funciones de transferencia nos permiten simular y evaluar el desempeño del sistema controlado antes de implementarlo en la práctica. Podemos utilizar herramientas de simulación numérica para obtener respuestas en frecuencia, respuestas transitorias y analizar la estabilidad del sistema con diferentes configuraciones de controladores.

Las funciones de transferencia son una herramienta indispensable en el diseño de controladores de sistemas. Nos permiten comprender el comportamiento de un sistema sin necesidad de conocer todos sus detalles internos. Mediante el análisis de la función de transferencia, podemos diseñar controladores efectivos, simular el comportamiento del sistema y evaluar su desempeño antes de implementarlo en la práctica. Si deseas mejorar tus habilidades en el diseño de controladores, es fundamental entender y utilizar de manera efectiva las funciones de transferencia.

Cuáles son las limitaciones y consideraciones al utilizar funciones de transferencia en la práctica

Al utilizar funciones de transferencia en la práctica, es importante tener en cuenta algunas limitaciones y consideraciones que pueden afectar su efectividad. A continuación, se detallan algunos puntos clave a tener en cuenta:

1. Linealidad

Las funciones de transferencia asumen una relación lineal entre la entrada y la salida de un sistema. Sin embargo, en muchos casos reales, la relación puede ser no lineal. Es crucial comprender las limitaciones de la linealidad al utilizar funciones de transferencia y considerar alternativas si es necesario.

2. Variabilidad del sistema

Es posible que los sistemas reales varíen con el tiempo debido a diversos factores, como el desgaste, las condiciones ambientales o la variabilidad natural. Estas variaciones pueden afectar la precisión y la estabilidad de las funciones de transferencia utilizadas. Por lo tanto, es importante monitorear y ajustar regularmente las funciones de transferencia para minimizar los errores causados por estos cambios.

3. Aproximación y discreción

Hay casos en los que es necesario aproximar teóricamente la función de transferencia real debido a limitaciones prácticas o a la necesidad de simplificar el modelo matemático utilizado. Además, muchas veces la información disponible solo permite obtener la función de transferencia en forma discreta, lo que puede introducir errores o limitaciones adicionales. En estas situaciones, es fundamental comprender los posibles efectos de la aproximación y discreción en los resultados obtenidos.

4. Estabilidad y respuesta transitoria

Al diseñar y utilizar funciones de transferencia, es crucial considerar la estabilidad del sistema y su respuesta transitoria. Algunos sistemas pueden ser inherentemente inestables o tener una respuesta transitoria no deseada, lo que puede afectar el rendimiento y la eficacia de las funciones de transferencia utilizadas. Es indispensable realizar pruebas y realizar ajustes adecuados para garantizar la estabilidad y obtener la respuesta transitoria deseada.

5. Condiciones de contorno y restricciones

Es importante tener en cuenta las condiciones de contorno y las restricciones específicas del sistema al usar funciones de transferencia. Algunos sistemas pueden tener limitaciones físicas, técnicas o prácticas que deben considerarse al seleccionar y aplicar funciones de transferencia. Estas condiciones y restricciones pueden afectar significativamente la relación entre la entrada y la salida del sistema, por lo que deben ser analizadas y tenidas en cuenta en el proceso.

Si bien las funciones de transferencia son herramientas poderosas para comprender y utilizar sistemas dinámicos, es fundamental tener en cuenta las limitaciones y consideraciones discutidas anteriormente. Al estar consciente de estas cuestiones, se puede aprovechar al máximo el potencial de las funciones de transferencia y utilizarlas de manera efectiva en la práctica.

Cuáles son ejemplos comunes de aplicaciones prácticas de funciones de transferencia en diferentes campos de la ingeniería

Las funciones de transferencia son herramientas fundamentales en el campo de la ingeniería. Su uso se extiende a diversas áreas, tanto en aplicaciones teóricas como prácticas. A continuación, exploraremos algunos ejemplos comunes de cómo se utilizan las funciones de transferencia en diferentes campos de la ingeniería.

1. Ingeniería eléctrica y electrónica:

En este campo, las funciones de transferencia son esenciales para analizar y diseñar circuitos eléctricos y electrónicos. Por ejemplo, en el diseño de filtros activos, las funciones de transferencia permiten modelar y evaluar la respuesta en frecuencia del circuito. Además, en sistemas de control, las funciones de transferencia se utilizan para representar los elementos del sistema y analizar su estabilidad y desempeño.

2. Ingeniería mecánica:

En la ingeniería mecánica, las funciones de transferencia encuentran aplicación en el análisis y diseño de sistemas dinámicos. Por ejemplo, en el estudio de vibraciones de estructuras, las funciones de transferencia permiten modelar la respuesta del sistema ante excitaciones externas. Asimismo, en el diseño de sistemas de suspensión o amortiguación, las funciones de transferencia son utilizadas para analizar el comportamiento del sistema y ajustar sus parametros para mejorar su rendimiento.

3. Ingeniería química:

En la ingeniería química, las funciones de transferencia son empleadas en diversas áreas, como la cinética de reacciones químicas y el diseño de procesos. Por ejemplo, en el estudio de reactores químicos, las funciones de transferencia permiten modelar y analizar la evolución de las concentraciones de los reactivos y productos en función del tiempo. Además, en el diseño de sistemas de control de procesos químicos, las funciones de transferencia ayudan a comprender y optimizar el comportamiento del sistema.

4. Ingeniería civil:

En la ingeniería civil, las funciones de transferencia se aplican en áreas como la dinámica de estructuras y el análisis de sistemas de transporte. Por ejemplo, en el diseño de puentes o edificios, las funciones de transferencia permiten evaluar y predecir la respuesta estructural ante cargas estáticas y dinámicas. En el campo del análisis de tráfico y transporte, las funciones de transferencia son utilizadas para modelar el flujo vehicular y analizar el rendimiento de carreteras y sistemas de transporte público.

5. Ingeniería de sistemas:

En este campo interdisciplinario, las funciones de transferencia son empleadas para analizar y diseñar sistemas complejos. Por ejemplo, en el estudio de sistemas de comunicación, las funciones de transferencia permiten evaluar la calidad de la señal y analizar la propagación de ondas electromagnéticas. Asimismo, en el diseño de sistemas de control automático, las funciones de transferencia representan la relación entre las entradas y salidas del sistema, lo que facilita su análisis y diseño.

Estos son solo algunos ejemplos de cómo las funciones de transferencia se utilizan en diferentes campos de la ingeniería. Su versatilidad y aplicabilidad hacen de estas herramientas una parte esencial de la formación y el trabajo de los ingenieros en diversas disciplinas.

Preguntas frecuentes (FAQ)

1. ¿Qué es una función de transferencia?

Una función de transferencia es una herramienta matemática que describe la relación entre la entrada y la salida de un sistema dinámico.

2. ¿Para qué sirve una función de transferencia?

Una función de transferencia permite analizar y predecir el comportamiento de un sistema en función de sus condiciones iniciales y su entrada.

3. ¿Qué información proporciona una función de transferencia?

Una función de transferencia proporciona información sobre las características del sistema, como estabilidad, amortiguamiento, resonancia, entre otros.

4. ¿Cómo se representa una función de transferencia?

Una función de transferencia se suele representar con la letra "H" y un subíndice que indica la entrada y otro que indica la salida del sistema. Por ejemplo, H(s) representa la función de transferencia de un sistema en función de la variable compleja s.

5. ¿Cómo se utiliza una función de transferencia en la práctica?

Una función de transferencia se puede utilizar para diseñar y analizar controladores en sistemas eléctricos, mecánicos, químicos, entre otros.