¡Descubre cuántos décimos hay en 1 unidad! Aprende sobre la relación entre 5 y 10

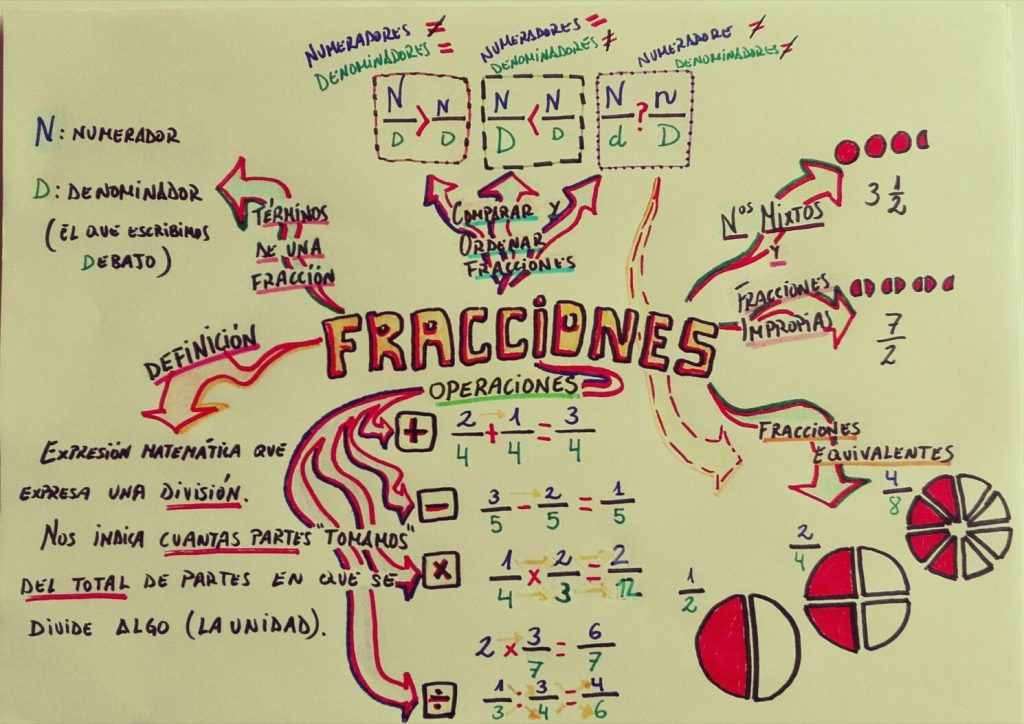
El concepto de fracciones es fundamental<strong> en matemáticas, ya que nos permite representar partes de un todo. Una fracción puede expresarse como una división entre dos números, donde el numerador<strong> representa la cantidad de partes que se toman y el denominador<strong> indica la cantidad total en la que se divide el todo. Exploraremos específicamente las fracciones equivalentes<strong> a 1 unidad y cómo podemos relacionarlas con los números 5<strong> y 10<strong>.

A lo largo del texto, veremos ejemplos y explicaciones para comprender mejor la relación entre las fracciones<strong> y los números enteros<strong>. Conoceremos la equivalencia entre fracciones y décimos<strong>, y entenderemos cuántas veces podemos dividir la unidad para obtener una fracción determinada. Además, veremos cómo podemos simplificar fracciones<strong> y trabajar con múltiples factores de la unidad. Al finalizar, tendrás una sólida comprensión de cómo reconocer y utilizar adecuadamente estas relaciones en problemas matemáticos.

Cuál es el concepto de "décimo" y cómo se relaciona con las unidades

Los décimos son una forma de representar partes igualmente divididas de una unidad. En otras palabras, si dividimos una unidad en diez partes iguales, cada una de estas partes se denomina "décimo". Esto nos permite tener una manera más precisa de medir y expresar cantidades que no son enteras.

La relación entre los décimos y las unidades es fundamental para comprender su funcionalidad. Para ello, debemos entender que un "décimo" es una fracción que representa una décima parte de una unidad. Así como el número 1 representa una unidad completa, el número 0.1 representa un "décimo" de esa unidad.

Para visualizarlo mejor, podemos imaginar una línea recta que representa la unidad. Dividimos esta línea en diez partes iguales y marcamos cada una de ellas como un "décimo". De esta manera, tenemos una escala donde podemos ubicar cualquier cantidad entre 0 y 1 en función de los "décimos".

La importancia de los "décimos" en el sistema decimal

El sistema decimal es el sistema numérico más utilizado en todo el mundo, y los "décimos" juegan un papel crucial en él. La base del sistema decimal es el número 10, lo que significa que utilizamos diez dígitos distintos (del 0 al 9) para representar cualquier cantidad. Los "décimos" nos permiten expresar valores intermedios entre estos dígitos.

Por ejemplo, si queremos representar el número 5 en el sistema decimal, podemos hacerlo simplemente escribiendo el dígito 5. Sin embargo, si queremos representar un valor más preciso, digamos 5.5, necesitamos utilizar los "décimos". En este caso, el número 5 representa cinco unidades completas y el número 0.5 representa cinco "décimos" de esa unidad.

Esto es especialmente útil en situaciones donde necesitamos medir cantidades que no son enteras, como en las fracciones o los porcentajes. Los "décimos" nos permiten desglosar una unidad en partes más pequeñas y expresar con precisión cuántas de esas partes están presentes.

Aplicaciones prácticas de los "décimos"

Los "décimos" tienen aplicaciones prácticas en diversas áreas, como la matemática, la física, la economía y muchas otras disciplinas. Algunos ejemplos de cómo se utilizan los "décimos" en estos campos incluyen:

• Conversión de fracciones a decimales: Las fracciones pueden representarse como una combinación de números enteros y "décimos". Por ejemplo, la fracción 3/10 se puede escribir como el número decimal 0.3. Esto facilita las operaciones matemáticas con fracciones, ya que podemos utilizar las propiedades del sistema decimal para simplificar y calcular más fácilmente.
• Mediciones precisas: En la física y otras ciencias, a menudo necesitamos medir cantidades que no son enteras. Los "décimos" nos permiten expresar estas medidas de manera más precisa. Por ejemplo, si queremos medir la masa de un objeto con una balanza, podemos obtener valores como 1.3 kg o 0.7 kg utilizando los "décimos" como parte de nuestra unidad de medida.
• Cálculos financieros: En el ámbito económico, los "décimos" son esenciales para realizar cálculos financieros precisos. Por ejemplo, si estamos calculando intereses sobre un préstamo o inversiones, necesitamos expresar tasas de interés en términos de "décimos" para obtener resultados exactos.

Los "décimos" son una forma de representar partes igualmente divididas de una unidad. Su relación con las unidades es crucial para entender su funcionalidad y cómo se utilizan en el sistema decimal. Los "décimos" tienen aplicaciones prácticas en diversos campos y nos permiten expresar valores más precisos y realizar cálculos más exactos en situaciones donde las cantidades no son enteras.

Cuántos décimos hay en una unidad completa

La relación entre los décimos y las unidades completas es fundamental en el sistema decimal. Para comprender cuántos décimos hay en una unidad completa, debemos recordar primero cómo está estructurado el sistema de numeración decimal.

En el sistema decimal, tenemos diez dígitos diferentes que van del 0 al 9: 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9. Estos dígitos se combinan para formar números más grandes utilizando la posición de cada dígito en el número.

¿Qué es una unidad completa?

Una unidad completa representa un número entero sin ninguna parte decimal. Es decir, cuando no tenemos ninguna fracción o decimal adicionales. En otras palabras, una unidad completa es simplemente un número entero que no tiene ningún añadido después de la coma decimal.

Por ejemplo, el número 7 es una unidad completa, ya que no tiene ningún decimal ni fracción agregados. Por otro lado, el número 7.5 no es una unidad completa, ya que tiene un decimal agregado (el ".5" representa medio).

La relación entre 5 y 10

Para comprender cuántos décimos hay en una unidad completa, debemos analizar la relación entre el número 5 y el número 10. En el sistema decimal, el número 10 representa una unidad completa, ya que no tiene ningún decimal adicional.

Si dividimos una unidad completa en 10 partes iguales, cada una de esas partes sería un décimo (1/10) de la unidad completa. Tomando esto en cuenta, podemos decir que un décimo (1/10) es igual a 0.1 en notación decimal.

Esta relación nos lleva a la conclusión de que hay 10 décimos en una unidad completa, ya que tenemos 10 partes iguales (cada una siendo un décimo).

Una unidad completa representa un número entero sin ninguna parte decimal o fracción adicional. Para entender cuántos décimos hay en una unidad completa, debemos considerar la relación entre el número 5 y el número 10. Si dividimos una unidad completa en 10 partes iguales, cada una de esas partes sería un décimo (0.1 en notación decimal). Por lo tanto, podemos concluir que hay 10 décimos en una unidad completa.

Qué significa que un número tiene 5 décimos

Los números decimales son aquellos que tienen una parte entera y una parte decimal. La parte decimal se expresa utilizando una coma o un punto y representa una fracción del número total. Cuando decimos que un número tiene 5 décimos, nos referimos a que su parte decimal representa 5/10 o 1/2 del número total.

Para entender mejor esta relación entre 5 y 10, es importante recordar que el número 10 es considerado la unidad base en nuestro sistema decimal. Esto significa que todas las medidas y fracciones se comparan con la unidad base de 10. Si un número tiene 5 décimos, esto indica que su parte decimal se divide en 10 partes iguales y que estamos tomando la mitad de esa división, es decir, 5 partes.

Cómo se representa 5 décimos

En la representación numérica, los décimos se escriben después de la coma o el punto en una cifra decimal. Por ejemplo, si tenemos el número 1,5, esto significa que tenemos 1 unidad y medio/dos décimos. Para representar solo los 5 décimos sin la parte entera, se utiliza la expresión "0,5". Es importante tener en cuenta que cuando trabajamos con números decimales, siempre debemos indicar la unidad seguida de la coma o punto para diferenciarlos de los números enteros.

La equivalencia entre décimos y fracciones

Los décimos también se pueden expresar como una fracción común. En este caso, 5 décimos se representa como 5/10. Sin embargo, si queremos simplificar esta fracción, podemos dividir tanto el numerador como el denominador por su máximo común divisor, que en este caso es 5. Al hacerlo, obtenemos como resultado la fracción 1/2, lo cual significa que 5 décimos es equivalente a la mitad.

Es importante comprender esta relación entre los números decimales y las fracciones, ya que ambos representan la misma cantidad, aunque se expresen de manera diferente. Los décimos nos permiten dividir una unidad en partes iguales para obtener una fracción específica del total.

Aplicaciones prácticas de los décimos

La idea de los décimos es muy útil en muchas áreas de la vida cotidiana. Por ejemplo, cuando vamos al supermercado y compramos frutas o verduras, a menudo la cantidad se mide y se vende en kilos. Pero si sólo queremos comprar una parte de un kilo, podemos utilizar los décimos. Si deseamos comprar media kilo de manzanas, estamos comprando 5 décimos de un kilo.

Otro ejemplo común es el uso de los décimos en el sistema monetario. Cuando hablamos de centavos, podemos pensar en ellos como décimos de una moneda. Por ejemplo, si tenemos 50 centavos, esto es equivalente a tener 5 décimos de un peso. Los décimos nos permiten calcular y entender mejor el valor de una fracción de una unidad monetaria.

La noción de los décimos es fundamental para comprender cómo se divide una unidad en partes iguales en nuestro sistema decimal. Entender que 5 décimos es igual a la mitad nos ayuda a visualizar mejor la relación entre los números decimales y las fracciones, y nos permite aplicar esta noción en diferentes situaciones cotidianas.

Cómo se puede representar la relación entre 5 y 10 utilizando décimos

La relación entre 5 y 10 es un concepto fundamental en matemáticas. Para comprenderla mejor, es útil explorar cómo se puede representar esta relación utilizando décimos. En este artículo, vamos a descubrir cuántos décimos hay en 1 unidad y cómo esto nos ayudará a comprender la relación entre 5 y 10.

En matemáticas, los décimos son una forma de fracción decimal que se utiliza para dividir una unidad en 10 partes iguales. Cada una de estas partes se denomina décimo, ya que representa una décima parte de la unidad completa. Si tomamos una unidad completa y la dividimos en 10 décimos, cada décimo sería equivalente a 0.1, lo que significa que habría 10 décimos en total.

Entonces, ¿cómo podemos relacionar esto con los números 5 y 10? Bueno, imaginemos que queremos representar el número 5 utilizando décimos. Podemos hacer esto tomando la unidad completa y dividiéndola en 10 partes iguales. Como sabemos que hay 10 décimos en una unidad, podemos decir que 5 es igual a la mitad de esa cantidad, es decir, 5 décimos.

Representando 5 utilizando décimos:

1. Tenemos una unidad.
2. Dividimos esa unidad en 10 partes iguales, obteniendo 10 décimos en total.
3. Tomamos la mitad de esa cantidad, lo que resulta en 5 décimos.

De manera similar, podemos hacer uso de los décimos para representar el número 10. Si tomamos la unidad completa y la dividimos en 10 partes iguales, obtendríamos 10 décimos. En este caso, no necesitamos tomar una fracción de esa cantidad, ya que el número 10 es igual a la totalidad de los 10 décimos.

Representando 10 utilizando décimos:

1. Tenemos una unidad.
2. Dividimos esa unidad en 10 partes iguales, obteniendo 10 décimos en total.
3. El número 10 es igual a la totalidad de los 10 décimos

Ahora bien, ¿qué pasa si queremos representar un número entre 5 y 10 utilizando décimos? Bueno, eso dependerá específicamente del número que estamos tratando de representar.

Supongamos que queremos representar el número 7 utilizando décimos. Podemos empezar dividiendo la unidad completa en 10 partes iguales, lo que nos daría 10 décimos en total. Luego, simplemente contaríamos 7 décimos desde el comienzo para obtener la representación decimal de 7 en décimos.

Los décimos nos permiten representar números de manera fraccionaria y decimal. Al dividir una unidad en 10 partes iguales, podemos utilizar los décimos para expresar diferentes cantidades, incluyendo aquellos números que están entre 5 y 10. Esta representación nos ayuda a comprender mejor la relación entre estos dos números y cómo se pueden desglosar en partes más pequeñas.

Cuál es la fracción equivalente a 5 décimos

Para comprender cuál es la fracción equivalente a 5 décimos, es necesario recordar que una cantidad decimal se puede representar como una fracción en donde el denominador es una potencia de 10. En este caso, los décimos son una unidad dividida en diez partes iguales, por lo que podemos escribirlo como 1/10.

Ahora bien, si deseamos encontrar una fracción equivalente a 5 décimos, simplemente debemos buscar una fracción en la que el numerador sea un múltiplo de 5, pero que mantenga el mismo denominador de 10.

Una forma sencilla de lograr esto es multiplicar tanto el numerador como el denominador por el mismo número. Si multiplicamos 1/10 por 5, obtendremos (1*5)/(10*5), lo cual simplificado resulta en 5/50.

Entonces, la fracción equivalente a 5 décimos es 5/50. Esta fracción aún puede simplificarse dividiendo tanto el numerador como el denominador por su máximo común divisor, que en este caso es 5. Al hacerlo, obtenemos 1/10.

5 décimos es igual a la fracción 1/10. Esto significa que si tenemos una unidad y queremos repartirla en décimas partes, cada una de esas partes será equivalente a 1/10 de la unidad total.

Cómo se puede expresar 10 como una combinación de unidades y décimos

Para comprender cómo se puede expresar 10 como una combinación de unidades y décimos, primero debemos entender qué significa exactamente esto. En matemáticas, la unidad se refiere a un número entero, mientras que los décimos representan una fracción decimal de una unidad.

Entonces, cuando hablamos de combinar unidades y décimos para expresar 10, nos referimos a encontrar diferentes combinaciones de números enteros y fracciones decimales que sumen un total de 10.

Una forma común de representar 10 usando unidades y décimos es mediante el uso de la notación decimal. En este sistema, un número decimal se separa en dos partes: la parte entera y la parte decimal. La parte entera representa las unidades completas, mientras que la parte decimal representa las fracciones de la unidad.

Por ejemplo, podemos expresar 10 como 10 unidades completas o como 10.0 en notación decimal. Sin embargo, también podemos representar 10 de otras formas utilizando una combinación de números enteros y decimales.

Ejemplo 1: 9 unidades y 1 décimo

Una forma de representar 10 es usando 9 unidades completas y 1 décimo. En este caso, tenemos 9 números enteros que representan las unidades completas y 1 número decimal que representa una fracción de la unidad.

En notación decimal, esto sería expresado como 9.1. Aquí, la parte entera (9) representa las unidades completas y la parte decimal (0.1) representa una fracción de la unidad.

Ejemplo 2: 10 unidades y 0 décimos

Otra forma de representar 10 es usando 10 unidades completas y 0 décimos. En este caso, no tenemos ninguna fracción de la unidad, por lo que todas las 10 partes del número son números enteros.

En notación decimal, esto sería expresado simplemente como 10. Aquí, no tenemos una parte decimal ya que no hay ninguna fracción de la unidad presente.

Ejemplo 3: 8 unidades y 2 décimos

Una tercera forma de representar 10 es usando 8 unidades completas y 2 décimos. En este caso, tenemos 8 números enteros que representan las unidades completas y 2 números decimales que representan dos fracciones de la unidad.

En notación decimal, esto sería expresado como 8.2. Aquí, la parte entera (8) representa las unidades completas y la parte decimal (0.2) representa dos fracciones de la unidad.

Estos ejemplos muestran solo algunas de las muchas formas en las que se puede expresar el número 10 utilizando diferentes combinaciones de unidades y décimos. Es importante tener en cuenta que estas representaciones son flexibles y pueden adaptarse a diferentes situaciones o contextos matemáticos.

Al comprender cómo se puede expresar 10 como una combinación de unidades y décimos, podemos desarrollar una mayor comprensión de los conceptos matemáticos y mejorar nuestras habilidades para trabajar con números decimales.

De qué manera se puede utilizar la relación entre 5 y 10 en problemas cotidianos

La relación entre 5 y 10 es una de las más utilizadas en problemas cotidianos. Esta relación se basa en la división de una unidad en partes iguales, conocidas como décimos. Un décimo es una fracción que representa una parte de diez. Específicamente, un décimo es igual a 1/10 o 0.1.

Para entender mejor esta relación, podemos pensar en un ejemplo práctico. Supongamos que tenemos una barra de chocolate que pesa 100 gramos. Si queremos dividir esa barra de chocolate en partes iguales, podemos utilizar la relación entre 5 y 10. Esto significa que vamos a dividir la barra en 10 partes iguales, lo cual nos dará segmentos de 10 gramos cada uno.

Si queremos saber cuántos décimos hay en 1 unidad, simplemente debemos recordar que una unidad está compuesta por 10 décimos. Por lo tanto, en el caso de nuestro ejemplo con la barra de chocolate, tendríamos que cada uno de los segmentos de 10 gramos representa un décimo de la unidad total de 100 gramos.

Esta relación entre 5 y 10 también puede ser útil en situaciones donde necesitamos calcular porcentajes. Por ejemplo, si queremos calcular el 50% de una cantidad, podemos utilizar la relación entre 5 y 10 para simplificar el cálculo. Sabemos que el 50% es la mitad de una cantidad, por lo que podemos multiplicar esa cantidad por la fracción 1/2, que equivale a 5/10.

Cómo utilizar la relación entre 5 y 10 en problemas de proporción

En problemas de proporción, la relación entre 5 y 10 puede ser muy útil para establecer equivalencias entre diferentes cantidades. Por ejemplo, si tenemos una proporción que dice que por cada 5 unidades de un producto necesitamos 10 unidades de otro, podemos utilizar esta relación para determinar cuántas unidades necesitamos en total.

Supongamos que queremos saber cuántos litros de agua necesitamos para preparar 5 tazas de té. Si sabemos que se necesita una proporción de 10 tazas de agua por cada 5 tazas de té, podemos utilizar la relación entre 5 y 10 para determinar el número de litros.

Si consideramos que una taza equivale a 0.2 litros, tenemos que por cada 0.2 litros necesitamos 10 tazas de agua. Para determinar cuántos litros necesitamos para las 5 tazas de té, simplemente debemos multiplicar 0.2 por 5 y dividirlo entre 10. El resultado será el número de litros necesario.

Utilizando la fórmula:

litros = (0.2 * 5) / 10

Obtendremos el valor de los litros necesarios. Esta es solo una aplicación básica de la relación entre 5 y 10 en problemas de proporción, pero la misma lógica se puede aplicar a situaciones más complejas donde se requiera resolver proporciones utilizando fracciones.

• La relación entre 5 y 10 es una herramienta muy útil en problemas cotidianos que involucran divisiones, porcentajes y proporciones.
• Permite dividir una unidad en partes iguales, conocidas como décimos, lo cual facilita el cálculo y la comprensión de las fracciones.
• También puede ser utilizada para simplificar cálculos de porcentajes, establecer equivalencias en problemas de proporción y resolver situaciones más complejas utilizando fracciones.

Comprender y utilizar la relación entre 5 y 10 nos ayuda a resolver problemas matemáticos y cotidianos de manera más eficiente y efectiva.

Cuál es la importancia de comprender los décimos al trabajar con medidas y fracciones

Los décimos son una parte fundamental de las medidas y las fracciones. Comprender su relación con otras unidades de medida, como los enteros, nos permite realizar operaciones matemáticas más precisas y eficientes.

En el sistema decimal, dividimos una unidad en diez partes iguales llamadas décimos. Podemos representar un décimo como 0.1 o 1/10. Aunque al principio puede parecer que una décima parte es muy pequeña, es esencial entender cómo se relacionan con otras unidades de medida y cómo afectan las fracciones.

Relación entre los décimos y los enteros

Los décimos son una forma de expresar una cantidad menor que uno entero. Por ejemplo, si tenemos una barra de chocolate y la dividimos en diez partes iguales, cada parte sería un décimo de la barra. Si tomamos dos de esas partes, tendríamos dos décimos, lo cual equivale a 0.2 o 2/10.

Es importante tener en cuenta que diez décimos son equivalentes a un entero. Esto significa que si tenemos diez partes de una unidad, tenemos una unidad completa. Podemos representar esto como 1.0 o simplemente 1.

La relación entre los décimos y los enteros nos permite realizar conversiones y cálculos más fácilmente. Por ejemplo, si queremos sumar 0.5 y 0.6, podemos convertirlos a décimos y luego sumarlos. Sería equivalente a sumar 5 décimos con 6 décimos, dando como resultado 11 décimos o 1.1.

Aplicaciones de los décimos en medidas y fracciones

Los décimos son especialmente útiles al trabajar con medidas precisas, como las relacionadas con el tiempo o las distancias. Por ejemplo, si queremos medir media hora, podemos representarla como 0.5 horas, lo cual equivale a 30 minutos.

También podemos utilizar los décimos al descomponer una unidad en fracciones. Si dividimos un entero en diez partes iguales, cada parte sería un décimo. Podemos expresar cualquier fracción que tenga 10 como denominador en términos de décimos. Por ejemplo, 3/10 representa tres décimos, mientras que 7/10 representa siete décimos.

Además, los décimos nos permiten ordenar y comparar números de manera más precisa. Si tenemos dos números decimales, podemos determinar cuál es mayor o menor comparando sus dígitos en la posición de los décimos.

Comprender la importancia de los décimos al trabajar con medidas y fracciones es esencial para desarrollar habilidades matemáticas sólidas. Los décimos nos ayudan a expresar cantidades menores que un entero, realizar conversiones y operaciones matemáticas más precisas, y comprender mejor la relación entre diferentes unidades de medida. Al dominar el concepto de los décimos, ampliamos nuestras capacidades para resolver problemas y manipular números de manera más eficiente.

Cómo podemos aplicar la relación entre 5 y 10 en situaciones de repartir o compartir cantidades

La relación entre 5 y 10 es una de las más básicas y fundamentales en las matemáticas. En esta sección, aprenderemos cómo podemos aplicar esta relación en situaciones de repartir o compartir cantidades.

Imaginemos que tenemos una unidad y queremos repartirla en partes iguales. En este caso, podemos pensar en la unidad como si fuese un pastel delicioso que queremos compartir con nuestros amigos. Si queremos dividir este pastel en 10 partes iguales, cada parte representará 1/10 de la unidad. Sin embargo, también podemos optar por dividir el pastel en 5 partes iguales, donde cada parte representa 1/5 de la unidad.

Ahora bien, ¿qué sucede si queremos repartir la unidad completa? Si elegimos dividir la unidad en 10 partes, obtendremos 10 décimos. Cada décimo será igual a 1/10 de la unidad. Por otro lado, si dividimos la unidad en 5 partes, obtendremos 5 quintos. Cada quinto representará 1/5 de la unidad.

Es importante destacar que, si bien tanto los décimos como los quintos representan una fracción de la unidad, existen diferencias entre ellos. Mientras que los décimos son más pequeños que los quintos, ya que hay más partes en las que se divide la unidad, los quintos son más grandes, ya que hay menos partes en las que se divide la unidad.

Ejemplo práctico:

Supongamos que tenemos una unidad de tiempo y queremos calcular cuántos décimos hay en ella. Si consideramos que esta unidad de tiempo equivale a 10 minutos, entonces cada décimo sería igual a 1 minuto. De esta manera, podemos decir que en una unidad de tiempo hay 10 décimos.

Por otro lado, si queremos calcular cuántos quintos hay en una unidad de tiempo, podríamos considerar que esta unidad equivale a 5 horas. En este caso, cada quinto sería igual a 1 hora. Por lo tanto, en una unidad de tiempo hay 5 quintos.

De esta forma, podemos observar cómo la relación entre 5 y 10 nos permite repartir o compartir cantidades de manera equitativa. Dependiendo de la situación, elegiremos dividir la unidad en 5 partes o en 10 partes, obteniendo así los quintos o los décimos correspondientes.

Qué ejemplos prácticos podemos encontrar en nuestra vida diaria que demuestren la relación entre 5 y 10 mediante décimos

La relación entre 5 y 10 mediante décimos es fundamental para comprender los conceptos matemáticos y su aplicación en nuestra vida diaria. A menudo, nos encontramos en situaciones donde necesitamos dividir una unidad completa en partes más pequeñas, y los décimos son una forma común de hacerlo.

Un ejemplo práctico que muestra esta relación es el sistema monetario. Si consideramos el euro como moneda, sabemos que 1 euro es igual a 100 céntimos. En este caso, cada céntimo representa una centésima parte del euro, lo cual implica que hay 100 décimos en una unidad completa.

Otro ejemplo de la relación entre 5 y 10 mediante décimos se encuentra en las fracciones decimales. Cuando se expresa una fracción con un denominador de 10 (como 3/10 o 7/10), estamos hablando de décimos. Estas fracciones representan una división de una unidad en 10 partes iguales, siendo cada parte igual a un décimo.

En términos más generales, la relación entre 5 y 10 también se puede ver en la escala decimal. El número 5 es la mitad de 10, lo cual significa que hay cinco décimos en medio de una unidad completa. Esta relación es especialmente útil cuando trabajamos con medidas o porcentajes.

Una manera de visualizar esta relación es a través de una recta numérica. Si dibujamos una recta que va desde el 0 hasta el 1, podemos marcar claramente los puntos correspondientes a los décimos. La marca del 0.5 representaría la mitad de la unidad, mientras que cada décimo subsecuente se puede marcar hasta llegar al 1.

La relación entre 5 y 10 mediante décimos es algo que encontramos en muchas áreas de nuestras vidas diarias, desde el sistema monetario hasta las fracciones decimales. Comprender esta relación nos permite descomponer una unidad completa en partes más pequeñas y realizar cálculos precisos. Además, nos ayuda a visualizar y entender mejor los conceptos matemáticos relacionados con la división y la escala decimal.

Preguntas frecuentes (FAQ)

1. ¿Cuántos décimos hay en 1 unidad?

En una unidad hay 10 décimos.

2. ¿Qué relación existe entre los números 5 y 10 en este contexto?

La relación es que 5 es la mitad de 10, por lo que cada décimo representa la mitad de una unidad.

3. ¿Cómo se representa un décimo en términos de fracción?

Un décimo se puede representar como 1/10.

4. ¿Qué es un decimal?

Un decimal es un número que utiliza la base 10 y tiene una parte decimal que representa una fracción de una unidad.

5. ¿Cuál es la diferencia entre un décimo y un centésimo?

La diferencia es que un décimo representa una parte de una unidad dividida en diez partes iguales, mientras que un centésimo representa una parte de una unidad dividida en cien partes iguales.