Descubre cómo sacar la base de un triángulo isósceles de forma rápida y sencilla

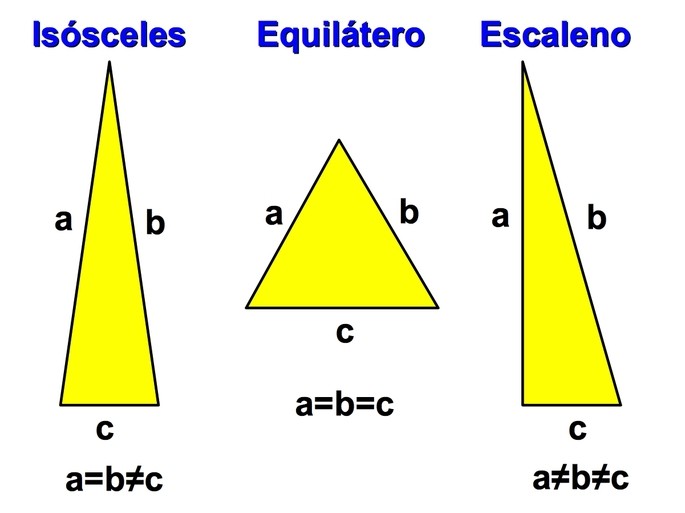
Los triángulos isósceles son aquellos que tienen dos lados iguales y un ángulo opuesto a estos lados también igual. Estos triángulos isósceles son muy comunes en la geometría y suelen presentarse en diversas situaciones. Sin embargo, en ocasiones puede resultar un poco complicado encontrar la medida de la base de un triángulo isósceles, especialmente si solo se conocen los ángulos o las medidas de los lados iguales. Por suerte, existen fórmulas y métodos para calcular la base de forma rápida y sencilla.

Te mostraremos paso a paso cómo puedes sacar la base de un triángulo isósceles utilizando diferentes enfoques. Veremos desde el método clásico utilizando trigonometría hasta otras alternativas más modernas como el uso de razones trigonométricas y proporciones. Además, te daremos ejemplos prácticos para que puedas aplicar los conceptos aprendidos. Así que si estás interesado en aprender cómo sacar la base de un triángulo isósceles, ¡sigue leyendo!

Qué es un triángulo isósceles y por qué es importante conocer su base

Un triángulo isósceles es un tipo de triángulo que tiene dos lados congruentes, es decir, que tienen la misma longitud, y un tercer lado que es diferente. La característica distintiva de este tipo de triángulo es que también tiene dos ángulos congruentes, lo que significa que tienen la misma medida.

Conocer la base de un triángulo isósceles es muy útil en diversos contextos matemáticos y geométricos. Por ejemplo, al resolver problemas relacionados con áreas de figuras geométricas, calcular perímetros o determinar las medidas de otros elementos del triángulo, como ángulos y diagonales.

Cómo sacar la base de un triángulo isósceles

Afortunadamente, encontrar la base de un triángulo isósceles es bastante sencillo, ya que podemos hacer uso del teorema de Pitágoras y algunas propiedades especiales de este tipo de triángulos.

Para sacar la base, necesitamos conocer la longitud de uno de los lados iguales y el ángulo formado por esos dos lados congruentes. Llamemos a este ángulo "α".

Una vez que tenemos estos datos, podemos aplicar el teorema de Pitágoras para obtener la longitud de la base. El teorema establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

En nuestro caso, al tener un triángulo isósceles, sabemos que el ángulo opuesto a la base (ángulo β) es congruente al ángulo α. Esto significa que el triángulo formado por la base y los dos lados iguales también es un triángulo isósceles.

Utilizando esta propiedad, podemos dividir nuestro triángulo isósceles en dos triángulos rectángulos adyacentes, donde la base es la hipotenusa de ambos triángulos y la mitad del lado igual es uno de los catetos.

Aplicando el teorema de Pitágoras a uno de los triángulos rectángulos, podemos encontrar la longitud de la base. Si llamamos a la longitud de uno de los lados iguales "a", entonces la longitud de la base (b) se calcula mediante la siguiente fórmula:

b = √(2 * a^2 - 2 * a^2 * cos(α))

Donde √ representa la raíz cuadrada y cos(α) es el coseno del ángulo α.

Una vez que tenemos la fórmula, solo necesitamos sustituir los valores conocidos y realizar las operaciones matemáticas correspondientes para obtener la longitud de la base del triángulo isósceles deseado.

Es importante mencionar que si ya conocemos la base del triángulo, también podemos utilizar la misma fórmula para calcular la longitud de los lados iguales o cualquier otro elemento del triángulo que necesitemos determinar.

La base de un triángulo isósceles se puede sacar aplicando el teorema de Pitágoras y utilizando las propiedades especiales de este tipo de triángulo. Conociendo la longitud de uno de los lados iguales y el ángulo formado por ellos, podemos calcular rápidamente la longitud de la base y utilizar esta información para resolver diversos problemas geométricos.

¿Cuáles son las propiedades principales de un triángulo isósceles?

Los triángulos isósceles son una de las figuras geométricas más comunes y fascinantes. Poseen propiedades únicas que los distinguen de otros tipos de triángulos y los convierten en objeto de estudio e interés tanto en matemáticas como en otras disciplinas.

Una de las principales características de un triángulo isósceles es que tiene dos lados iguales, lo cual implica que también tiene dos ángulos iguales opuestos a esos lados. Estos ángulos iguales se conocen como los ángulos de la base.

Otra propiedad importante es que los ángulos de la base siempre suman 180 grados, por lo que si conocemos uno de ellos, podemos calcular fácilmente el valor del otro. Esta propiedad es muy útil en muchos problemas y aplicaciones prácticas.

¿Cómo sacar la base de un triángulo isósceles?

Ahora que entendemos las propiedades fundamentales de un triángulo isósceles, vamos a explorar cómo podemos calcular la longitud de su base. Existen varias formas de hacerlo, dependiendo de qué información tenemos disponible.

1. Caso 1: Si conocemos las longitudes de los dos lados iguales y el ángulo comprendido entre ellos, podemos utilizar la ley de los cosenos para determinar la longitud de la base. La fórmula sería:

b = √(a^2 + a^2 - 2 * a * a * cos θ)

Donde b es la longitud de la base, a es la longitud de los lados iguales y θ es el ángulo comprendido entre ellos.

2. Caso 2: Si conocemos las longitudes de los dos lados iguales pero no el ángulo comprendido entre ellos, podemos utilizar la fórmula del seno para calcularlo. Una vez obtengamos el valor del ángulo, podemos usar el caso anterior para determinar la longitud de la base.

sin θ = (b/2) / a

Donde θ es el ángulo de la base, b es la longitud de la base y a es la longitud de los lados iguales.

3. Caso 3: Si conocemos la longitud de la base y uno de los ángulos de la base, podemos utilizar el conocimiento de que los ángulos de la base suman 180 grados para encontrar el valor del otro ángulo. Una vez tengamos ambos ángulos, podemos utilizar el caso 2 para determinar la longitud de los lados iguales.

θ + θ' = 180°

sin θ = (b/2) / a

Donde θ y θ' son los ángulos de la base, b es la longitud de la base y a es la longitud de los lados iguales.

Para calcular la longitud de la base de un triángulo isósceles es necesario conocer al menos dos de los siguientes elementos: las longitudes de los lados iguales, el ángulo comprendido entre ellos o uno de los ángulos de la base. A partir de esa información, podemos utilizar las fórmulas y propiedades mencionadas anteriormente para obtener el valor deseado.

Cómo puedo identificar la base de un triángulo isósceles

Identificar la base de un triángulo isósceles puede parecer complicado al principio, pero en realidad es bastante simple. Recuerda que un triángulo isósceles tiene dos lados iguales y un tercer lado diferente, llamado base. Aquí te mostraré cómo puedes identificar fácilmente la base de este tipo de triángulo.

Paso 1: Identifica los lados iguales del triángulo

Antes de poder encontrar la base, debemos identificar primero los lados iguales del triángulo. Estos son los dos lados que tienen la misma longitud. Puedes utilizar una regla o una cinta métrica para medir los lados si es necesario. Una vez que hayas encontrado los lados iguales, deberás señalarlos o recordar cuáles son.

Paso 2: Encuentra el vértice del triángulo

El vértice del triángulo es el punto donde se encuentran los dos lados iguales. Este punto es importante porque indica dónde se encuentra el ángulo superior del triángulo. Puedes marcar el vértice con un lápiz o cualquier otra herramienta que tengas a mano.

Paso 3: Traza una línea desde el vértice hasta el tercer vértice

Una vez que hayas identificado los lados iguales y el vértice del triángulo, ahora debes trazar una línea recta desde el vértice hasta el tercer vértice, el cual es el extremo opuesto a la base. Esta línea te ayudará a visualizar mejor la posición y longitud de la base.

Paso 4: Identifica la línea que une los extremos de los lados iguales

Por último, para encontrar la base del triángulo isósceles, debes identificar la línea que une los extremos de los lados iguales. Esta línea es paralela a la línea que trazaste en el paso anterior y tiene la misma longitud. Puedes marcar esta línea con una línea punteada o cualquier otra indicación para distinguirla claramente.

Ahora que has identificado la base del triángulo isósceles, podrás utilizar esta información en diferentes situaciones, como al calcular el área o aplicar el teorema de Pitágoras. Recuerda que la base es un elemento clave en la geometría de los triángulos isósceles, por lo que es importante saber cómo encontrarla correctamente.

Cuál es la fórmula para calcular el área de un triángulo isósceles

Calcular el área de un triángulo isósceles puede resultar fácil y rápido si conoces la fórmula adecuada. En este caso, vamos a enfocarnos en cómo obtener la medida de la base de un triángulo isósceles, ya que es un dato que muchas veces necesitamos conocer para resolver problemas geométricos.

La fórmula general para calcular el área de un triángulo es:

Área = (base x altura) / 2

Paso 1: Identificar la altura del triángulo

Antes de poder encontrar la base del triángulo isósceles, necesitamos conocer su altura. La altura de un triángulo isósceles es la perpendicular trazada desde el vértice opuesto a la base hasta dicha base.

Para encontrar la altura, puedes utilizar diferentes métodos dependiendo de la información que tengas. Si cuentas con las medidas de los lados y los ángulos, puedes utilizar la fórmula general:

Altura = (lado * seno(ángulo))

Donde "lado" corresponde a uno de los lados iguales del triángulo isósceles y "ángulo" es el ángulo que se forma entre la base y uno de los lados iguales.

Si no tienes la información completa, puedes utilizar otro método para encontrar la altura, como construir una perpendicular a la base desde el vértice opuesto utilizando una regla y un compás. Este método es especialmente útil cuando solo tienes la longitud de la base y los lados iguales.

Paso 2: Calcular la base del triángulo

Una vez que conoces la altura del triángulo isósceles, puedes utilizar la fórmula del área para despejar la base:

Base = (2 x Área) / Altura

Sustituyendo el valor del área y de la altura en la fórmula, podrás obtener la medida de la base del triángulo isósceles.

• Si la altura y el área están expresadas en las mismas unidades, el resultado de la base también será en esas unidades.
• Recuerda que la base de un triángulo isósceles siempre debe ser mayor a cero.

Ahora que conoces la fórmula y los pasos para obtener la base de un triángulo isósceles, podrás resolver problemas geométricos que involucren este tipo de figura. Recuerda que practicar con diferentes ejercicios te ayudará a fortalecer tus habilidades y comprender mejor los conceptos matemáticos.

Existen métodos alternativos para encontrar la base de un triángulo isósceles

Cuando nos encontramos con la tarea de calcular la base de un triángulo isósceles, es común recurrir a los métodos tradicionales que hemos aprendido en matemáticas. Sin embargo, existen enfoques alternativos que pueden resultar más rápidos y sencillos para resolver este problema geométrico.

Método 1: Utilizando el teorema de Pitágoras

Una forma de encontrar la base de un triángulo isósceles es utilizando el teorema de Pitágoras. Este teorema establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

En el caso de un triángulo isósceles, los dos catetos son congruentes, es decir, tienen la misma longitud. Por lo tanto, podemos considerar uno de los catetos como la base del triángulo y el otro cateto como la altura. Aplicando el teorema de Pitágoras, podemos encontrar la longitud de la base.

b = √(c^2 - h^2)

• b: longitud de la base
• c: longitud de los catetos (congruentes)
• h: altura del triángulo

Método 2: Utilizando las propiedades del triángulo isósceles

Otro enfoque para encontrar la base de un triángulo isósceles se basa en las propiedades de este tipo de triángulo. Recordemos que en un triángulo isósceles, los lados que no son la base son congruentes.

Si conocemos la longitud de uno de los lados congruentes y la altura del triángulo, podemos utilizar el Teorema de Pitágoras (como se explicó anteriormente) o el teorema de la altura para encontrar la longitud de la base.

b = 2 * √(c^2 - h^2)

• b: longitud de la base
• c: longitud de uno de los lados congruentes
• h: altura del triángulo

Método 3: Utilizando la fórmula general del área del triángulo

Otra forma de calcular la base de un triángulo isósceles es mediante el uso de la fórmula general del área de un triángulo. La fórmula del área del triángulo establece que el área es igual a la mitad del producto entre la base y la altura.

Despejando la base de esta fórmula, obtenemos:

b = 2 * (A / h)

• b: longitud de la base
• A: área del triángulo
• h: altura del triángulo

Estos son solo algunos métodos alternativos que puedes utilizar para encontrar la base de un triángulo isósceles. Como siempre, es importante tener en cuenta las condiciones y propiedades del problema particular que estés resolviendo.

Recuerda que la práctica y el conocimiento de diferentes métodos te permitirán tener una mayor comprensión y habilidad para resolver diversos problemas de geometría. ¡No dudes en explorar y experimentar con diferentes enfoques!

¿Cuáles son algunos consejos prácticos para sacar rápidamente la base de un triángulo isósceles?

Saber cómo sacar la base de un triángulo isósceles de forma rápida y sencilla puede ser de gran utilidad en diversos problemas geométricos. Pero, ¿qué es exactamente un triángulo isósceles? Un triángulo isósceles es aquel que tiene dos lados iguales y un ángulo opuesto a esos lados también igual. La base de un triángulo isósceles es precisamente el lado desigual.

Para sacar la base de un triángulo isósceles, podemos seguir algunos consejos prácticos que facilitarán este proceso. En primer lugar, si conocemos los valores del ángulo opuesto y uno de los lados iguales, podemos utilizar la trigonometría para encontrar el valor de la base. Aplicando la función seno o coseno, dependiendo del ángulo conocido, y utilizando las propiedades de los triángulos isósceles, podremos obtener el valor de la base rápidamente.

Ejemplo:


Si tenemos un triángulo isósceles con un ángulo opuesto de 45 grados y un lado igual de longitud 5 cm, podemos usar la función seno para encontrar la base.

sen(45°) = base / 5 cm

Resolviendo la ecuación:

base = sen(45°) * 5 cm


Otro método para sacar la base de un triángulo isósceles es utilizando el teorema de Pitágoras. Si conocemos los valores de los lados iguales y queremos encontrar la base, podemos utilizar el teorema de Pitágoras para calcularla. El teorema establece que en un triángulo rectángulo, el cuadrado de la hipotenusa (el lado más largo) es igual a la suma de los cuadrados de los otros dos lados. En un triángulo isósceles, la base y uno de los lados iguales forman un triángulo rectángulo, por lo que podemos aplicar el teorema de Pitágoras para encontrar la base.

Ejemplo:


Si tenemos un triángulo isósceles con un lado igual de longitud 3 cm, podemos utilizar el teorema de Pitágoras para encontrar la base.

base^2 + 3 cm^2 = 3 cm^2

Resolviendo la ecuación:

base^2 = 3 cm^2 - 3 cm^2

base^2 = 0 cm^2

base = sqrt(0 cm^2)


Es importante tener en cuenta que, en ocasiones, puede haber múltiples soluciones o no existir solución para sacar la base de un triángulo isósceles. Esto dependerá de las dimensiones del triángulo y las restricciones establecidas en el problema específico. En estos casos, se puede recurrir al uso de fórmulas más complejas, como la fórmula general del triángulo isósceles, o a métodos gráficos, como la construcción geométrica. Estos enfoques pueden requerir un mayor nivel de conocimiento y habilidad, pero también ofrecen una mayor precisión en determinadas situaciones.

Sacar la base de un triángulo isósceles puede ser rápido y sencillo si se utilizan los métodos adecuados. Ya sea a través de la trigonometría o del teorema de Pitágoras, podemos encontrar el valor de la base con facilidad. Sin embargo, es importante considerar las posibles limitaciones o condiciones adicionales de cada problema para obtener resultados precisos. ¡Así que no dudes en poner en práctica estos consejos y resolver problemas geométricos de manera eficiente!

¿Cómo puedo utilizar la base de un triángulo isósceles en situaciones cotidianas o problemas matemáticos?

La base de un triángulo isósceles es un elemento fundamental que se utiliza en diversas situaciones cotidianas y problemas matemáticos. Aprender a calcular y utilizar correctamente la base del triángulo isósceles puede resultar de gran utilidad para resolver una amplia variedad de situaciones prácticas y ejercicios teóricos.

¿Qué es un triángulo isósceles?

Antes de profundizar en el uso de la base de un triángulo isósceles, es importante comprender qué exactamente es este tipo de triángulo. Un triángulo isósceles es aquel que tiene dos lados de igual longitud y dos ángulos adyacentes de igual medida. Esto significa que las longitudes de los dos lados iguales son iguales entre sí, mientras que la longitud de la base es diferente.

Calculemos la base de un triángulo isósceles

Para calcular la base de un triángulo isósceles, necesitamos conocer la longitud de los lados iguales y el ángulo que forma la base con uno de los lados iguales. Para simplificar el cálculo, podemos utilizar la trigonometría y el teorema de Pitágoras.

Sea 'a' la longitud de los lados iguales del triángulo isósceles y 'b' la longitud de la base.

Aplicando el teorema de Pitágoras, podemos encontrar la longitud de la altura (h) del triángulo isósceles utilizando la fórmula:

h = √(a^2 - (b/2)^2)

Una vez que tenemos la longitud de la altura, podemos utilizar el ángulo formado entre la base y uno de los lados iguales para calcular la longitud de la base utilizando trigonometría. Supongamos que el ángulo es θ.

La fórmula para calcular la base sería:

b = 2 * h * tan(θ/2)

Aplicaciones prácticas de la base de un triángulo isósceles

La base de un triángulo isósceles tiene diversas aplicaciones prácticas en situaciones cotidianas y problemas matemáticos. Algunas de estas aplicaciones incluyen:

• Cálculo de áreas: La base del triángulo isósceles es necesaria para calcular el área del triángulo utilizando la fórmula A = (b * h) / 2, donde 'A' representa el área y 'h' la altura.
• Geometría: La base se utiliza para determinar la congruencia y similitud de triángulos isósceles en problemas relacionados con la geometría.
• Resolución de problemas trigonométricos: El cálculo de la base puede ayudarnos a resolver problemas que involucren funciones trigonométricas como el seno, coseno y tangente.

La base de un triángulo isósceles es un elemento clave que se utiliza en diversas situaciones prácticas y problemas matemáticos. Saber calcular y utilizar correctamente la base nos permite resolver problemas de áreas, geometría y trigonometría. Además, comprender las propiedades del triángulo isósceles y cómo se relaciona su base con los otros elementos nos brinda una mayor comprensión de la geometría y sus aplicaciones prácticas.

Qué recursos adicionales existen para aprender más sobre triángulos isósceles y sus propiedades

Los triángulos isósceles son una figura geométrica muy interesante y es importante comprender sus propiedades para poder resolver problemas relacionados con ellos. Afortunadamente, existen muchos recursos adicionales disponibles que te pueden ayudar a aprender más sobre triángulos isósceles y mejorar tus habilidades en este tema.

1. Libros de matemáticas

Los libros de texto de matemáticas suelen abordar los conceptos básicos de los triángulos isósceles y proporcionar ejemplos y ejercicios prácticos para practicar. Estos libros son una excelente opción para aquellos que prefieren un enfoque más tradicional y estructurado para el aprendizaje.

2. Tutoriales en línea

Internet está lleno de tutoriales en línea gratuitos que cubren una amplia gama de temas matemáticos, incluidos los triángulos isósceles. Puedes encontrar videos explicativos, ejercicios resueltos paso a paso y quiz interactivos que te permiten poner en práctica lo aprendido. Algunas plataformas populares que ofrecen estos recursos son Khan Academy, Coursera y YouTube.

3. Aplicaciones móviles

Si prefieres aprender sobre la marcha, hay muchas aplicaciones móviles disponibles que pueden ayudarte a estudiar los triángulos isósceles. Estas aplicaciones suelen tener lecciones interactivas, ejercicios de práctica y juegos educativos para hacer el aprendizaje más divertido y entretenido.

4. Sitios web especializados

Existen sitios web especializados en matemáticas y geometría que se enfocan específicamente en los triángulos isósceles. Estos sitios pueden proporcionar explicaciones más detalladas, ejemplos adicionales y pruebas de evaluación para ayudarte a fortalecer tus conocimientos en este tema.

5. Comunidades en línea

Otra forma excelente de aprender sobre triángulos isósceles es unirse a comunidades en línea donde podrás interactuar con otros estudiantes y profesionales de las matemáticas. Puedes hacer preguntas, compartir ideas y obtener ayuda de personas que comparten tu interés en este tema. Algunas comunidades populares incluyen foros en línea, grupos de estudio en redes sociales y plataformas de tutoría virtual.

No importa qué recurso adicional elijas utilizar, lo importante es tener una actitud abierta al aprendizaje y practicar regularmente. Cuanto más te sumerjas en el estudio de los triángulos isósceles, más confianza ganarás en resolver problemas relacionados con ellos. ¡No tengas miedo de explorar diferentes recursos y descubrir cuál es el mejor para ti!

Preguntas frecuentes (FAQ)

1. ¿Cómo puedo calcular la base de un triángulo isósceles?

Para calcular la base de un triángulo isósceles, puedes utilizar el teorema de Pitágoras o aplicar la fórmula de la altura del triángulo.

2. ¿Cuál es la fórmula para encontrar la base de un triángulo isósceles?

La fórmula para encontrar la base de un triángulo isósceles es: base = (2 * área) / altura

3. ¿Qué es un triángulo isósceles?

Un triángulo isósceles es aquel que tiene dos lados de igual longitud y dos ángulos adyacentes de igual medida.

4. ¿Cuáles son las propiedades de un triángulo isósceles?

Las principales propiedades de un triángulo isósceles son: tiene dos lados iguales, tiene dos ángulos iguales y la altura desde el vértice hasta la base divide al triángulo en dos triángulos congruentes.

5. ¿Cuáles son los elementos necesarios para calcular la base de un triángulo isósceles?

Los elementos necesarios para calcular la base de un triángulo isósceles son: la longitud de uno de los lados iguales y la altura del triángulo.