Descubre cómo identificar si una función es inyectiva y evita errores matemáticos

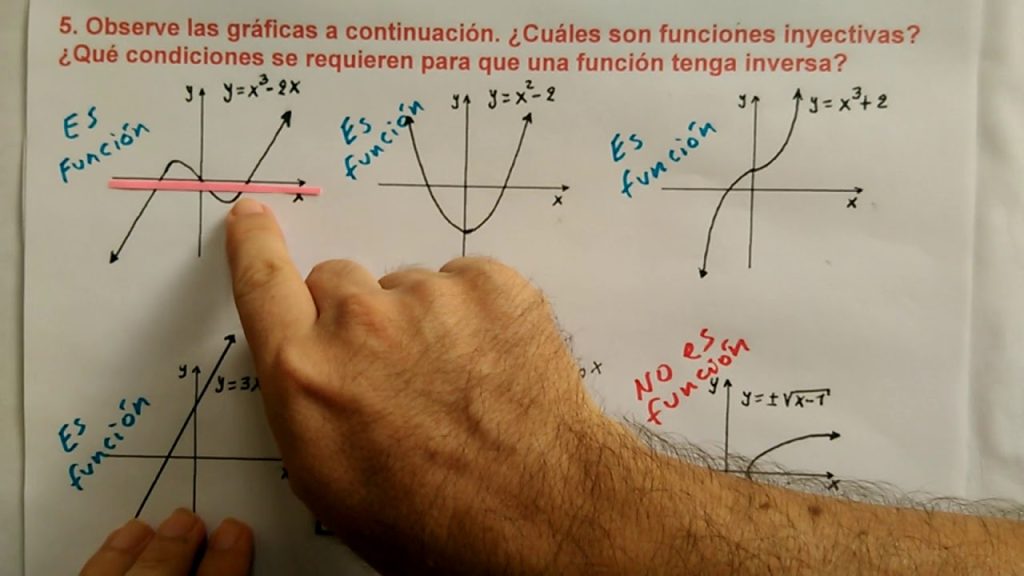
En matemáticas, una función es una relación entre dos conjuntos que asigna a cada elemento del primer conjunto (dominio) un único elemento del segundo conjunto (codominio). Dicho de otra manera, una función establece una correspondencia entre los elementos de dos conjuntos. El estudio de las propiedades de las funciones es fundamental en el ámbito de las matemáticas y permite comprender mejor cómo se relacionan diferentes variables o magnitudes.

Una propiedad importante que se puede analizar en una función es si es inyectiva. Una función inyectiva, también conocida como función uno a uno, cumple con la condición de que cada elemento del dominio se corresponde con un único elemento del codominio. En otras palabras, no existen dos elementos distintos del dominio que tengan la misma imagen en el codominio. A lo largo de este artículo, analizaremos cómo identificar si una función es inyectiva y veremos ejemplos para comprender mejor esta propiedad matemática.

Qué es una función inyectiva y por qué es importante en matemáticas

Una función inyectiva, también conocida como función uno a uno, es una función matemática que asigna cada elemento del dominio a un único elemento del codominio. En otras palabras, no existen dos elementos diferentes en el dominio que se asignen al mismo elemento en el codominio.

Para comprender mejor la importancia de las funciones inyectivas en matemáticas, es necesario entender cómo funcionan las funciones en general. Una función es una relación entre dos conjuntos, el conjunto de entrada (dominio) y el conjunto de salida (codominio), que asigna cada elemento del dominio a un único elemento del codominio.

A diferencia de las funciones en general, las funciones inyectivas tienen una propiedad adicional: cada elemento en el conjunto de salida está asociado a lo sumo con un único elemento en el conjunto de entrada. Es decir, si un elemento del codominio tiene más de un elemento en el dominio que se le asigna, entonces la función no puede ser inyectiva.

Una forma común de determinar si una función es inyectiva es mediante el uso de una prueba de la negación. Para demostrar que una función no es inyectiva, basta con encontrar al menos un par de elementos diferentes en el dominio que se asignen al mismo elemento en el codominio.

Las funciones inyectivas son importantes en diversos campos de las matemáticas, como el análisis real y el álgebra lineal. En el análisis real, por ejemplo, las funciones inyectivas son utilizadas para definir conceptos fundamentales como límites, continuidad y derivabilidad. En el álgebra lineal, las funciones inyectivas juegan un papel crucial en la resolución de sistemas de ecuaciones lineales y en el estudio de espacios vectoriales.

Una función es inyectiva si asigna cada elemento del dominio a un único elemento en el codominio. Determinar si una función es inyectiva puede ser importante para evitar errores matemáticos y para comprender mejor conceptos fundamentales en diversas ramas de las matemáticas.

Cuáles son las características de una función inyectiva

Una función se considera inyectiva cuando cada elemento del dominio se asigna a un único elemento en el rango. En otras palabras, no puede haber dos elementos diferentes en el dominio que tengan la misma imagen en el rango.

Para identificar si una función es inyectiva, podemos seguir algunos pasos sencillos:

1. Paso 1: Verificar si todos los elementos del dominio tienen una imagen en el rango.

Esto implica revisar meticulosamente cada elemento del dominio y comprobar si existe algún elemento en el rango que se asigna a él. Si todos los elementos del dominio tienen una imagen única en el rango, entonces podemos decir que la función es inyectiva.

2. Paso 2: Comprobar si no existen elementos repetidos en el rango.

Si hay algún elemento en el rango que se asigna a más de un elemento en el dominio, entonces la función no es inyectiva. La presencia de elementos repetidos en el rango indica que hay al menos dos elementos distintos en el dominio que se asignan al mismo elemento en el rango.

3. Paso 3: Analizar si la gráfica de la función pasa la "prueba de la recta vertical".

La "prueba de la recta vertical" consiste en trazar líneas verticales en la gráfica de la función. Si ninguna línea intersecta la gráfica en más de un punto, entonces la función es inyectiva. Si encontramos alguna línea vertical que intersecta la gráfica en más de un punto, entonces la función no es inyectiva.

Es importante tener en cuenta que estos pasos son solo una guía general y pueden variar dependiendo del contexto y las particularidades de cada función. Además, existen propiedades y teoremas adicionales que pueden ayudarnos a demostrar o refutar si una función es inyectiva en casos más complejos.

Ejemplos de funciones inyectivas

A continuación, presentamos algunos ejemplos de funciones inyectivas para ilustrar mejor el concepto:

• f(x) = x + 2

En esta función, cualquier valor asignado a x tiene una única imagen en el rango, ya que sumarle 2 a cualquier número produce un resultado diferente.

• g(x) = 3x

Esta función también es inyectiva, ya que cualquier valor que se le asigne a x tendrá una única imagen en el rango al multiplicarlo por 3.

• h(x) = x2

En este caso, la función no es inyectiva, ya que valores positivos y negativos tienen la misma imagen en el rango cuando se elevan al cuadrado.

Identificar si una función es inyectiva implica verificar que cada elemento del dominio tenga una única imagen en el rango, que no existan elementos repetidos en el rango y que la gráfica de la función pase la "prueba de la recta vertical". Siguiendo estos pasos y ejemplos, podrás evitar errores matemáticos al determinar si una función es inyectiva.

Cómo puedo identificar si una función es inyectiva

La inyectividad es un concepto fundamental en las matemáticas, especialmente cuando se trata de funciones. Identificar si una función es inyectiva puede ser clave para evitar errores y malentendidos en tus cálculos y aplicaciones matemáticas.

Una función se considera inyectiva cuando cada elemento del dominio está asignado a un único elemento en el rango, es decir, no existen dos elementos distintos en el dominio que sean mapeados al mismo elemento en el rango. En otras palabras, no puede haber repeticiones en los valores asociados a los elementos del dominio.

Para determinar si una función es inyectiva, existen diferentes métodos y enfoques que puedes utilizar. A continuación, te presentamos algunas estrategias que te ayudarán a identificar si una función es inyectiva:

Método 1: Prueba de inyectividad

Este método consiste en demostrar o refutar la inyectividad de una función utilizando las definiciones y propiedades matemáticas fundamentales. Para ello, necesitarás tener un buen entendimiento de las propiedades de funciones y cómo estas se relacionan entre sí.

```
Ejemplo:

Dada la función f(x) = x^2

Si tomamos dos valores en el dominio, por ejemplo x = 2 y x = -2, obtenemos f(2) = 4 y f(-2) = 4 respectivamente. Aquí podemos observar que dos elementos distintos en el dominio están siendo mapeados al mismo elemento en el rango (f(2) = f(-2) = 4), lo que indica que la función f(x) = x^2 no es inyectiva.
```

Al realizar esta prueba para diferentes valores en el dominio, podrás determinar si una función es inyectiva o no.

Método 2: Uso de gráficas

Otra estrategia útil para identificar si una función es inyectiva es observar su representación gráfica. Si trazas la gráfica de la función y esta pasa la "prueba de la recta vertical", es decir, no intersecta más de una vez la misma línea vertical, entonces la función es inyectiva.

Por ejemplo, si graficamos la función f(x) = x^2, podemos ver que la parábola se abre hacia arriba y no intersecta una línea vertical más de una vez. Esto indica que la función es inyectiva.

Método 3: Análisis del dominio y rango

También puedes analizar el dominio y rango de una función para determinar si es inyectiva. Si cada elemento único en el dominio tiene un valor único asignado en el rango, entonces la función es inyectiva.

Por ejemplo, considera la función f(x) = 3x + 1. Al analizar el dominio, vemos que cualquier número real puede ser utilizado como entrada (dominio). Además, al calcular el rango, encontramos que todos los resultados posibles son distintos (no hay repeticiones). Por lo tanto, podemos concluir que la función f(x) = 3x + 1 es inyectiva.

La inyectividad de una función es fundamental en las matemáticas y puede evitarte errores y malentendidos en tus calculaciones. Utiliza los métodos mencionados anteriormente para identificar si una función es inyectiva y asegúrate de comprender sus propiedades y características clave.

Cuál es el método más común para demostrar que una función es inyectiva

Identificar si una función es inyectiva es fundamental en el campo de las matemáticas. Para demostrar que una función es inyectiva, el método más comúnmente utilizado es el análisis de la función y su relación con los elementos del dominio y el codominio.

El primer paso para demostrar que una función es inyectiva es comprender qué significa esta propiedad. Una función se considera inyectiva si cada elemento del dominio tiene un único elemento relacionado en el codominio. En otras palabras, no existen dos elementos distintos en el dominio que sean mapeados al mismo elemento en el codominio.

Para demostrar esto, podemos utilizar el método de análisis por contradicción. Supongamos que tenemos una función f(x) donde dos elementos distintos, digamos a y b en el dominio, son mapeados al mismo elemento c en el codominio.

Entonces, tendríamos f(a) = f(b) = c.

A partir de esta suposición, debemos demostrar que a = b, lo cual implicaría que no hay dos elementos distintos en el dominio que estén mapeados al mismo elemento en el codominio.

Para lograr esto, podemos asumir que a ≠ b y llegar a una contradicción lógica. Podemos comenzar analizando las propiedades de la función f(x) y su relación con los valores a, b y c.

Supongamos que a ≠ b y f(a) = f(b) = c. Si a ≠ b, entonces necesariamente debe haber una diferencia entre estos dos elementos. Si evaluamos f(a), obtendremos c, lo mismo ocurre si evaluamos f(b). Esto significa que a y b son mapeados al mismo valor en el codominio, lo cual contradice nuestra suposición inicial de que f(a) = f(b).

Por lo tanto, llegamos a la conclusión de que a = b, lo cual demuestra que no hay dos elementos distintos en el dominio que estén mapeados al mismo elemento en el codominio. Esto confirma que la función es inyectiva.

Es importante tener en cuenta que este es el método más comúnmente utilizado para demostrar que una función es inyectiva, pero existen otros enfoques y técnicas dependiendo del contexto matemático y las propiedades de la función en cuestión.

Existen casos en los que una función puede ser inyectiva pero no sea estrictamente creciente o decreciente

Cuando hablamos de funciones inyectivas, generalmente pensamos en aquellas que son estrictamente crecientes o decrecientes. Sin embargo, es importante tener en cuenta que existen casos en los que una función puede ser inyectiva pero no cumplir con esta condición.

Una función inyectiva es aquella en la que cada elemento del dominio se corresponde con un único elemento del codominio. Es decir, no hay dos elementos distintos en el dominio que tengan la misma imagen en el codominio.

En el contexto de las funciones matemáticas, solemos asociar la inyectividad con la monotonicidad, es decir, con la propiedad de ser estrictamente creciente o decreciente. Una función que es estrictamente creciente asigna a elementos mayores en el dominio imágenes mayores en el codominio, mientras que una función estrictamente decreciente asigna a elementos menores en el dominio imágenes menores en el codominio.

Por lo tanto, es fácil pensar que si una función es inyectiva, entonces debe ser estrictamente creciente o decreciente. Sin embargo, esto no siempre es cierto. Existen casos en los que una función cumple con la propiedad de inyectividad pero no es estrictamente creciente ni decreciente.

Un ejemplo clásico de este tipo de función es la función trigonométrica seno. El seno es una función periódica que oscila entre -1 y 1 en su dominio completo. A pesar de esto, el seno es una función inyectiva en diferentes intervalos de su dominio.

Ejemplo: Función seno inyectiva en el intervalo

Consideremos la función seno definida en el intervalo . Esta función es inyectiva en este intervalo porque para cada elemento del dominio hay una única imagen en el codominio.

Si graficamos esta función, veremos que se trata de una curva suave que oscila entre -1 y 1 a medida que avanzamos por el intervalo. A simple vista, puede parecer difícil creer que una función con estas características pueda ser inyectiva, pero esto se debe a que estamos acostumbrados a asociar la inyectividad con la monotonicidad.

La parte clave para comprender la inyectividad de la función seno en este intervalo es recordar que no debemos tener en cuenta el dominio completo de la función, sino el intervalo específico en el que estamos trabajando. Dentro de ese intervalo, la función seno cumple con la propiedad de inyectividad.

Es importante tener en cuenta que aunque solemos asociar la inyectividad con la monotonicidad en las funciones matemáticas, existen casos en los que una función puede ser inyectiva pero no necesariamente estrictamente creciente o decreciente. El ejemplo de la función seno en el intervalo nos ayuda a comprender mejor esta idea y evitar cometer errores matemáticos al identificar si una función es inyectiva o no.

Cuál es la importancia de evitar errores matemáticos al estudiar funciones inyectivas

Al estudiar funciones matemáticas, es fundamental tener una comprensión clara de los conceptos y propiedades asociadas a ellas. Un error común que suele ocurrir al trabajar con funciones es confundir si una función es inyectiva o no. Identificar correctamente si una función es inyectiva es esencial en muchos contextos, como el análisis de la relación entre conjuntos y la resolución de problemas prácticos.

Una función inyectiva, también conocida como uno a uno, es aquella en la que cada elemento del dominio se asigna a un único elemento del codominio. Esto significa que dos elementos distintos del dominio no pueden mapearse en el mismo elemento del codominio. Por lo tanto, si una función no cumple esta propiedad, se considera no inyectiva.

Evitar errores matemáticos al identificar si una función es inyectiva es crucial para realizar correctos razonamientos y demostraciones. Si se comete un error al determinar si una función es inyectiva, todas las conclusiones posteriores basadas en esa suposición errónea serán incorrectas. Esto puede llevar a resultados completamente equivocados en problemas prácticos o en investigaciones científicas.

1. Uno de los errores más frecuentes es confundir inyectividad con surjectividad. Estos dos conceptos son diferentes y cada uno tiene su propia definición y características particulares. Un buen entendimiento de ambos es vital para evitar confusiones.
2. Otro error común es evaluar la inyectividad de una función sin prestar atención adecuada a sus componentes. Una función puede parecer inyectiva a simple vista, pero al analizar sus características más específicas se pueden identificar casos en los que no lo es. Es importante tener en cuenta todos los elementos involucrados para evitar errores de interpretación.
3. La falta de comprensión de los conceptos y propiedades fundamentales de las funciones también puede llevar a errores. Por ejemplo, no entender cómo se aplica la propiedad del dominio codominio puede dificultar la correcta determinación de si una función es inyectiva o no.

Para evitar estos errores, es recomendable adquirir un sólido conocimiento de los principios básicos de las funciones y sus propiedades. Estudiar ejemplos concretos y practicar la aplicación de los conceptos en problemas reales puede ayudar a fortalecer la comprensión y evitar malentendidos. Además, consultar fuentes confiables de información matemática y buscar asesoramiento de profesores o tutores también es una estrategia útil para asegurarse de estar llevando a cabo los razonamientos correctamente.

Qué tipos de errores matemáticos son comunes al analizar funciones inyectivas

Al analizar una función para determinar si es inyectiva, es común cometer errores matemáticos que pueden llevarte a conclusiones incorrectas. Es importante conocer estos errores y saber cómo evitarlos para realizar un análisis adecuado.

Error de interpretación de la definición

Uno de los errores más comunes es interpretar equivocadamente la definición de una función inyectiva. Una función se considera inyectiva si cada elemento del dominio se asigna a un único elemento en el codominio. Sin embargo, muchas veces se confunde la unicidad con la existencia de una correspondencia uno a uno entre los elementos. Es importante recordar que una función puede ser inyectiva aunque no todos los elementos del codominio estén asignados.

Error en el análisis algebraico

Otro error frecuente al analizar funciones inyectivas es cometer fallos en las operaciones algebraicas. Al simplificar expresiones o resolver ecuaciones, es fácil deslizarse y cometer errores de cálculo. Estos errores pueden llevar a deducciones incorrectas sobre la inyectividad de la función.

Inconsistencia en el rango

Un error común es asumir que el rango de una función inyectiva es igual a su conjunto imagen. El conjunto imagen está formado por todos los elementos en el codominio que son imágenes de algún elemento en el dominio, mientras que el rango está formado solo por los elementos que son realmente alcanzados por la función. Si se confunden ambos conceptos, se pueden cometer errores al identificar si la función es inyectiva.

No considerar restricciones del dominio

Un error fatal es no considerar las restricciones del dominio al analizar la inyectividad de una función. Algunas funciones son inyectivas solo cuando se restringe el dominio a ciertos valores. Si no se toman en cuenta estas restricciones, se pueden llegar a conclusiones incorrectas sobre la inyectividad de la función.

Espero que esta información te sea útil para identificar y evitar los errores matemáticos comunes al analizar si una función es inyectiva. Recuerda siempre revisar cuidadosamente tus razonamientos y verificar todas las etapas de tu análisis para obtener resultados precisos.

Cuáles son algunas estrategias para evitar errores al identificar si una función es inyectiva

A la hora de identificar si una función es inyectiva, es importante tener en cuenta algunas estrategias que pueden ayudarnos a evitar errores matemáticos. La inyectividad de una función es una propiedad fundamental en el análisis matemático, ya que nos permite determinar si existe o no una correspondencia uno a uno entre los elementos del dominio y los del codominio de la función. En esta sección, exploraremos algunas técnicas y consejos útiles para asegurarnos de que estamos identificando correctamente la inyectividad de una función.

1. Analizar el dominio y codominio de la función

Antes de comenzar a evaluar la inyectividad de una función, es imprescindible tener claro cuál es su dominio y codominio. El dominio se refiere al conjunto de valores que pueden tomar las variables independientes de la función, mientras que el codominio representa el conjunto de valores que pueden tomar las variables dependientes.

Es vital asegurarse de que la función esté definida adecuadamente en todo su dominio, ya que cualquier valor no permitido podría generar ambigüedad en la evaluación de la inyectividad. Además, es necesario conocer el rango de la función, es decir, los valores que toma realmente en su codominio, para poder compararlos correctamente con los del dominio.

2. Investigar la existencia de reversibilidad

Una estrategia útil para determinar la inyectividad de una función es verificar si existe reversibilidad en la relación entre los elementos del dominio y los del codominio. La función es inyectiva si para cada pareja de elementos distintos del dominio, sus imágenes en el codominio también son diferentes.

Podemos investigar la existencia de reversibilidad realizando una prueba sencilla. Tomamos dos elementos distintos del dominio, por ejemplo, x1 y x2, y evaluamos la función en ambos valores. Si obtenemos dos imágenes diferentes, es un indicativo de que la función puede ser inyectiva. Sin embargo, es importante recordar que este método no es suficiente para demostrar la inyectividad, ya que debemos realizar pruebas exhaustivas con todos los posibles pares de elementos del dominio.

3. Utilizar el método del contrarrecíproco

Otra técnica efectiva para determinar si una función es inyectiva es utilizar el método del contrarrecíproco. Este método se basa en la propiedad de que si dos imágenes son iguales, entonces los elementos correspondientes en el dominio también son iguales.

Para aplicar el método del contrarrecíproco, asumimos que dos imágenes de la función son iguales, es decir, f(x1) = f(x2). Luego, mediante manipulación algebraica, llegamos a la conclusión de que x1 = x2. Si podemos demostrar que el supuesto inicial de igualdad de las imágenes implica necesariamente la igualdad de los elementos del dominio, podemos afirmar que la función es inyectiva.

4. Estudiar la derivada de la función

En casos más avanzados, cuando la función es diferenciable, podemos utilizar el estudio de la derivada para determinar la inyectividad. En particular, si la derivada de la función es siempre positiva o siempre negativa en todo su dominio, entonces la función es estrictamente creciente o estrictamente decreciente, respectivamente.

La propiedad de ser estrictamente creciente o decreciente implica que no pueden existir dos elementos distintos del dominio con la misma imagen en el codominio, lo cual conduce a la conclusión de que la función es inyectiva.

Es importante destacar que esta estrategia solo se puede aplicar en funciones diferenciables y que es necesario conocer las propiedades fundamentales de la derivada para su correcta utilización.

Para identificar si una función es inyectiva sin cometer errores matemáticos, debemos analizar cuidadosamente su dominio y codominio, investigar la existencia de reversibilidad, utilizar el método del contrarrecíproco cuando sea posible y estudiar la derivada en casos más avanzados. Al utilizar estas estrategias, podemos asegurarnos de determinar con precisión si una función es inyectiva o no, evitando así errores en nuestros análisis y cálculos matemáticos.

Cuáles son las consecuencias de cometer errores al identificar si una función es inyectiva

Cuando se trabaja con funciones matemáticas, es crucial poder identificar si una función es inyectiva de manera precisa. La inyectividad es una propiedad muy importante que puede tener una función y su correcta identificación tiene diversas implicaciones en el ámbito matemático.

Identificar correctamente si una función es o no inyectiva implica evitar cometer errores que puedan llevar a conclusiones erróneas y a problemas en la resolución de problemas matemáticos más complejos.

Consecuencias de no identificar correctamente si una función es inyectiva:

• Error en la resolución de sistemas de ecuaciones: Cuando se trabaja con sistemas de ecuaciones, la inyectividad de las funciones involucradas juega un papel fundamental. Si se comete un error al identificar si alguna de las funciones en el sistema es inyectiva, la solución obtenida puede ser incorrecta y conducir a resultados inconsistentes o contradictorios.
• Problemas en el análisis de gráficas: Las funciones inyectivas tienen una característica especial en sus gráficas: no pueden intersectarse en ningún punto horizontalmente. Identificar incorrectamente si una función es inyectiva puede llevar a interpretar erróneamente los puntos de intersección en una gráfica, lo que dará lugar a un análisis impreciso y a conclusiones equivocadas.
• Dificultades en la demostración de proposiciones matemáticas: En muchos casos, demostrar si una función es inyectiva o no es un paso crucial para demostrar proposiciones matemáticas más complejas. Si no se identifica correctamente la inyectividad de una función, la demostración de una proposición puede quedar invalidada y llevar a errores en la teoría matemática.
• Confusión en la clasificación de funciones: Las funciones inyectivas son solo una de las muchas clasificaciones que pueden tener las funciones matemáticas. Si no se logra identificar con precisión si una función es inyectiva, su clasificación puede resultar ambigua o incorrecta, lo que a su vez afectará el estudio y comprensión de conceptos matemáticos más avanzados.

Cometer errores al identificar si una función es inyectiva puede tener consecuencias negativas en diferentes ramas de las matemáticas. Por esta razón, es importante contar con un entendimiento claro de qué significa la inyectividad y cómo determinarla correctamente. La práctica y el estudio cuidadoso de los conceptos relacionados son clave para evitar este tipo de errores y garantizar un desarrollo sólido de habilidades matemáticas.

Hay recursos útiles disponibles en línea para aprender más sobre funciones inyectivas

Si estás estudiando matemáticas y te encuentras con el concepto de funciones inyectivas, es importante entender cómo identificar si una función específica cumple con esta propiedad. Una función inyectiva es aquella en la que cada elemento del conjunto de partida tiene asociado un único elemento del conjunto de llegada, es decir, no existen elementos distintos en el conjunto de partida que se asignen al mismo elemento en el conjunto de llegada.

Identificar si una función es inyectiva puede resultar un desafío para algunos estudiantes, pero afortunadamente hay muchos recursos útiles disponibles en línea que pueden ayudarte a comprender este concepto y evitar errores comunes en el proceso.

1. Sitios web especializados en matemáticas

Existen numerosos sitios web especializados en matemáticas que ofrecen explicaciones detalladas y ejemplos prácticos sobre funciones inyectivas. Estos sitios suelen incluir contenido didáctico, videos tutoriales y ejercicios interactivos que te permitirán practicar tus habilidades en la identificación de funciones inyectivas. Algunos de estos sitios incluso cuentan con foros de discusión donde puedes intercambiar ideas y resolver dudas junto a otros estudiantes y profesores expertos en matemáticas.

2. Tutoriales en video

Otra opción muy beneficiosa son los tutoriales en video. Existen canales de YouTube o plataformas educativas en línea que cuentan con profesores que explican paso a paso cómo identificar si una función es inyectiva. Estos videos suelen ser una forma más visual y dinámica de aprender, ya que puedes ver en tiempo real la aplicación de los conceptos y resolver ejercicios junto al profesor.

3. Libros de texto especializados

Los libros de texto especializados en matemáticas también son una fuente invaluable de conocimiento. Estos libros suelen contener teoría detallada, ejemplos resueltos y ejercicios propuestos que te permiten practicar la identificación de funciones inyectivas. Además, muchos de estos libros incluyen respuestas o soluciones a los ejercicios para que puedas verificar tus resultados y corregir posibles errores.

4. Grupos de estudio y tutorías personalizadas

No subestimes el poder del aprendizaje colaborativo. Unirse a grupos de estudio o recibir tutorías personalizadas puede ser de gran ayuda para comprender mejor las funciones inyectivas. Al trabajar con otros estudiantes o recibir la guía de un tutor experimentado, puedes discutir ideas, resolver problemas juntos y recibir retroalimentación instantánea. Esto te ayudará a aclarar cualquier duda que tengas y consolidar tus conocimientos sobre funciones inyectivas.

Identificar si una función es inyectiva requiere práctica y comprensión adecuada del concepto. Aprovecha los recursos disponibles en línea, como sitios web especializados en matemáticas, tutoriales en video, libros de texto y grupos de estudio para mejorar tus habilidades en la identificación de funciones inyectivas. Recuerda que evitar errores matemáticos depende de tu dedicación y disposición para aprender constantemente.

Preguntas frecuentes (FAQ)

1. ¿Qué significa que una función sea inyectiva?

Una función es inyectiva cuando cada elemento del dominio se relaciona con un único elemento en el codominio.

2. ¿Cómo puedo determinar si una función es inyectiva?

Para determinar si una función es inyectiva, puedes utilizar el método de la prueba de uno a uno, donde analizas si cada par de elementos diferentes en el dominio se relacionan con diferentes elementos en el codominio.

3. ¿Existe alguna forma visual de identificar si una función es inyectiva?

Sí, es posible visualizar si una función es inyectiva en un gráfico. Si una línea horizontal sólo atraviesa al gráfico de la función una vez en cualquier punto, entonces es inyectiva.

4. ¿Cuál es la importancia de determinar si una función es inyectiva?

Determinar si una función es inyectiva es importante para garantizar que no existan repeticiones en las correspondencias entre los elementos de los conjuntos involucrados, lo cual puede facilitar el análisis y resolución de problemas matemáticos.

5. ¿Cuáles son las consecuencias de usar incorrectamente el término "inyectiva"?

Usar incorrectamente el término "inyectiva" puede llevarte a cometer errores en tus cálculos matemáticos o en la interpretación de resultados, ya que puede generar confusiones con otros conceptos como funciones suryectivas y biyectivas, que son distintos.