Descubre cómo calcular el área del triángulo escaleno de forma sencilla y precisa

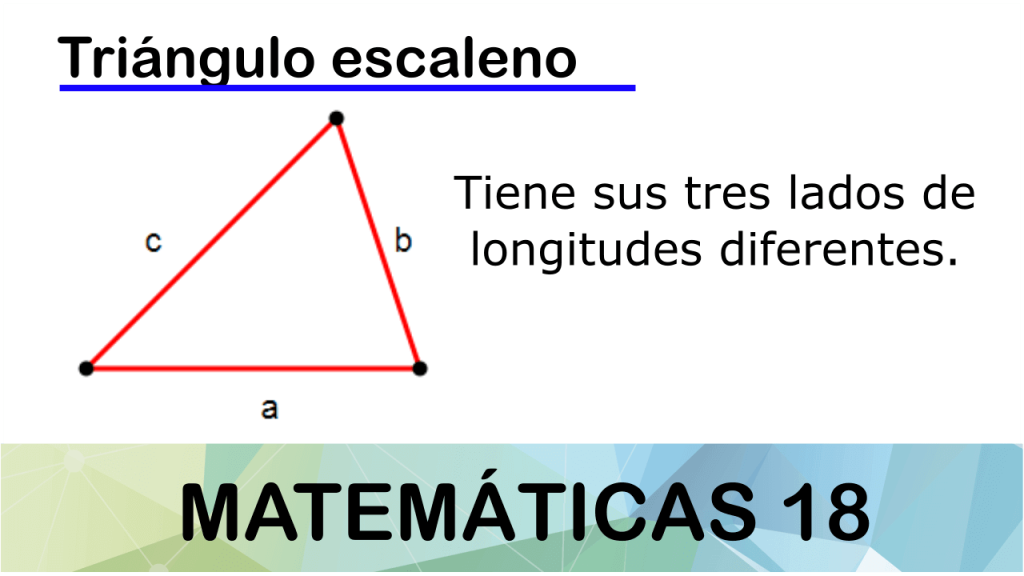
El triángulo es una de las figuras geométricas más básicas y utilizadas en matemáticas. Existen diferentes tipos de triángulos, como el equilátero, isósceles o escaleno, cada uno con sus propiedades particulares.

Te explicaremos cómo calcular el área de un triángulo escaleno de forma sencilla y precisa. Te daremos la fórmula matemática necesaria y te mostraremos un ejemplo paso a paso para que puedas aplicarlo fácilmente en tus ejercicios o problemas de geometría.

Cuáles son las características del triángulo escaleno

El triángulo escaleno es un tipo de figura geométrica que se caracteriza por tener tres lados de longitudes diferentes y tres ángulos internos también distintos. A diferencia del triángulo equilátero, donde todos los lados miden lo mismo, y del triángulo isósceles, donde dos lados son iguales, el triángulo escaleno presenta una asimetría en sus elementos.

Para identificar un triángulo como escaleno, es necesario que ninguno de sus lados sea igual en longitud a los otros dos. Además, sus ángulos internos tampoco serán iguales entre sí. Esto da lugar a una figura cuyas proporciones pueden variar dependiendo de las medidas de sus lados y ángulos, lo que le confiere una apariencia más versátil y variada.

Aunque pueda parecer menos común que otros tipos de triángulos, el triángulo escaleno está presente en muchas situaciones cotidianas. Por ejemplo, las formas irregulares encontradas en la naturaleza, como las costas de una playa o las siluetas de las montañas, suelen estar compuestas por triángulos escalenos. Además, este tipo de triángulo también puede ser utilizado en la construcción de estructuras arquitectónicas o en el diseño de objetos de arte.

Cómo calcular el área de un triángulo escaleno

Calcular el área de un triángulo escaleno es una tarea relativamente sencilla si se conocen las medidas de sus lados. Para ello, puedes utilizar la fórmula de Herón, que es un método general para calcular el área de un triángulo sin conocer la altura. La fórmula es la siguiente:

Área = √(s(s - a)(s - b)(s - c))

Donde s representa el semiperímetro del triángulo, definido como la suma de la longitud de los tres lados dividida entre 2; y a, b y c son las longitudes de los lados del triángulo.

Una vez que obtengas el valor del área utilizando esta fórmula, tendrás la superficie del triángulo escaleno en unidades cuadradas. Es importante recordar que todas las medidas empleadas deben estar expresadas en la misma unidad de longitud para obtener un resultado preciso.

Si conoces además la altura del triángulo, también puedes utilizar la fórmula tradicional para calcular el área (base por altura dividido por 2), siempre y cuando conozcas la base correspondiente al lado paralelo a la altura.

El triángulo escaleno es una figura geométrica versátil y asimétrica, cuyo cálculo del área puede realizarse mediante la fórmula de Herón o la fórmula tradicional del triángulo. Conociendo las medidas adecuadas, podrás determinar la superficie de esta figura con precisión. Ahora que sabes cómo calcular el área de un triángulo escaleno, ¡ponlo en práctica y sigue explorando el fascinante mundo de la geometría!

Cuál es la fórmula para calcular el área de un triángulo escaleno

Calcular el área de un triángulo escaleno puede parecer complicado a primera vista, pero en realidad es un proceso sencillo si conoces la fórmula adecuada. Un triángulo escaleno es aquel en el que sus tres lados tienen longitudes diferentes y ninguno de sus ángulos es igual.

La fórmula para calcular el área de un triángulo escaleno es mediante la fórmula de Herón, también conocida como la fórmula semiperimétrica. Esta fórmula se basa en el semiperímetro del triángulo, que se obtiene sumando las longitudes de los tres lados y dividiendo el resultado entre 2.

Una vez que tengamos el semiperímetro, se puede aplicar la fórmula de Herón:


Área = √(s(s - a)(s - b)(s - c))


Donde "s" representa el semiperímetro del triángulo y "a", "b" y "c" son las longitudes de los tres lados. La operación de √ denota la raíz cuadrada del resultado obtenido al multiplicar los tres términos dentro del paréntesis.

Por ejemplo, supongamos que tenemos un triángulo escaleno con lados de longitud 6 cm, 9 cm y 12 cm. Calcularemos primero el semiperímetro:


Semiperímetro = (6 + 9 + 12) / 2 = 27 / 2 = 13.5 cm


Ahora podemos aplicar la fórmula de Herón para encontrar el área:


Área = √(13.5(13.5 - 6)(13.5 - 9)(13.5 - 12))
= √(13.5(7.5)(4.5)(1.5))
≈ √1125.5625
≈ 33.54 cm²


Entonces, el área de este triángulo escaleno es aproximadamente 33.54 cm².

Vale la pena mencionar que la fórmula de Herón funciona para cualquier tipo de triángulo, no solo para los escalenos. Sin embargo, en el caso de triángulos equiláteros o isósceles, existen fórmulas más simples y directas para calcular su área.

Ahora que conoces la fórmula adecuada, el cálculo del área de un triángulo escaleno será una tarea mucho más fácil y precisa. Solo necesitarás conocer las longitudes de sus tres lados y aplicar la fórmula de Herón. ¡Inténtalo por ti mismo y comprueba lo sencillo que puede ser!

Cuáles son los pasos para calcular el área de un triángulo escaleno

Calcular el área de un triángulo escaleno puede parecer complicado, pero en realidad es mucho más sencillo de lo que piensas. En esta sección, te revelaremos los pasos necesarios para calcular el área de este tipo de triángulo de forma precisa y sin complicaciones.

Paso 1: Obtén las medidas de los lados del triángulo

Lo primero que debes hacer es obtener las medidas de los lados del triángulo escaleno. Recuerda que en un triángulo escaleno, todos sus lados tienen longitudes distintas. Por ejemplo, podrías tener un triángulo con lados de 7 cm, 9 cm y 12 cm.

Paso 2: Calcula el semiperímetro del triángulo

El semiperímetro de un triángulo se calcula sumando las longitudes de los tres lados y dividiendo el resultado entre 2. Utilizando el ejemplo anterior, tendríamos:

Semiperímetro = (7 cm + 9 cm + 12 cm) / 2 = 14 cm

Paso 3: Aplica la fórmula de Herón

La fórmula de Herón es una fórmula matemática utilizada para calcular el área de un triángulo a partir de las longitudes de sus lados. Se expresa de la siguiente manera:

Área = √(s * (s - a) * (s - b) * (s - c))
Donde:

• a, b, c son las longitudes de los lados del triángulo.
• s es el semiperímetro del triángulo.

Utilizando nuestro ejemplo y sustituyendo los valores en la fórmula, tendríamos:

Área = √(14 cm * (14 cm - 7 cm) * (14 cm - 9 cm) * (14 cm - 12 cm)) = √(14 cm * 7 cm * 5 cm * 2 cm) ≈ 21.54 cm²

Paso 4: ¡El área del triángulo escaleno es...

¡Listo! Ahora conoces los pasos para calcular el área de un triángulo escaleno. En nuestro ejemplo, el área aproximada del triángulo con lados de 7 cm, 9 cm y 12 cm sería de aproximadamente 21.54 cm².

Ten en cuenta que este método solo aplica para triángulos escalenos. Si tienes un triángulo equilátero o isósceles, deberás utilizar otras fórmulas específicas para calcular su área.

Recuerda siempre verificar tus cálculos y practicar con diferentes ejemplos para afianzar tus conocimientos. ¡Prueba con más triángulos escalenos y desafía tus habilidades matemáticas!

Qué información necesito para realizar el cálculo del área

Para calcular el área de un triángulo escaleno, necesitaremos contar con tres medidas específicas: la longitud de sus tres lados. Estos pueden ser cualquier número real y no tienen que ser iguales entre sí.

Es importante tener en cuenta que si solo conocemos dos lados del triángulo, no será posible calcular su área de manera precisa. Los tres lados deben ser proporcionados para realizar el cálculo correctamente.

Usando la fórmula de Herón

La fórmula más comúnmente utilizada para calcular el área de un triángulo escaleno es la fórmula de Herón, la cual se basa en el teorema de Herón. Esta fórmula es especialmente útil cuando conocemos las longitudes de los tres lados del triángulo.

La fórmula es la siguiente:

A = √(s(s - a)(s - b)(s - c))

Donde A representa el área del triángulo y a, b y c representan las longitudes de los tres lados del triángulo. Además, s es el semiperímetro del triángulo, definido como la suma de los tres lados dividida por 2:

s = (a + b + c) / 2

Una vez que tengamos todas estas medidas, simplemente sustituimos en la fórmula y realizamos los cálculos correspondientes para obtener el área final.

Ejemplo práctico

Supongamos que tenemos un triángulo escaleno con lados de longitud a = 6, b = 8 y c = 10. Para calcular el área, primero necesitamos obtener el semiperímetro s:

s = (6 + 8 + 10) / 2 = 24 / 2 = 12

Ahora, utilizando la fórmula de Herón, podemos calcular el área:

A = √(12(12 - 6)(12 - 8)(12 - 10)) = √(12 * 6 * 4 * 2) = √(576) = 24

Por lo tanto, el área de este triángulo escaleno es de 24 unidades cuadradas.

Ten en cuenta que si los lados del triángulo no son números enteros, es importante manejar correctamente los decimales en cada cálculo para obtener resultados precisos.

Otras fórmulas para calcular el área

Además de la fórmula de Herón, existen otras fórmulas que también se pueden utilizar para calcular el área de un triángulo escaleno si conocemos ciertos datos adicionales. Algunas de estas fórmulas incluyen el uso de ángulos y alturas del triángulo.

Es recomendable tener en cuenta estas alternativas, ya que podrían ser útiles en casos específicos donde no es posible obtener todas las longitudes de los lados del triángulo.

• Por ejemplo, si conocemos la longitud de un lado y el ángulo opuesto a ese lado, podemos utilizar la fórmula:

A = (1/2) * a * b * sen(C)

• Donde a y b son las longitudes de los dos lados adyacentes al ángulo C, y sen(C) es el seno de dicho ángulo.
• Otra fórmula útil es la del área utilizando una altura:

A = (1/2) * base * altura

• Donde base es la longitud de uno de los lados del triángulo y altura es la distancia perpendicular entre dicho lado y la base que forma un ángulo recto.

Estas fórmulas adicionales pueden resultar valiosas en diferentes situaciones y podrían brindarte alternativas para realizar el cálculo del área si no tienes todos los datos de los lados del triángulo escaleno.

Calcular el área de un triángulo escaleno puede parecer un proceso complicado, especialmente cuando no se conocen todas las medidas de sus lados. Sin embargo, con la fórmula de Herón y otras fórmulas adicionales, es posible obtener resultados precisos incluso ante estas limitaciones.

Recuerda que la clave está en recopilar la información correcta sobre los lados del triángulo y aplicar las fórmulas correspondientes. Con un poco de práctica, podrás realizar estos cálculos de forma sencilla y precisa, ¡logrando así resolver problemas geométricos relacionados con triángulos escalenos!

Cuál es la importancia de calcular el área del triángulo escaleno

Calcular el área del triángulo escaleno es una habilidad básica en la geometría que se utiliza en varios campos, como la arquitectura, la ingeniería y las ciencias naturales. El área de un triángulo es fundamental para determinar la superficie que ocupa, lo cual puede ser de vital importancia al diseñar estructuras o analizar fenómenos naturales.

El triángulo escaleno es aquel que tiene sus tres lados de longitudes diferentes. A diferencia del triángulo equilátero o isósceles, no hay una fórmula general que permita calcular directamente su área. Sin embargo, conociendo la longitud de los lados y aplicando una sencilla fórmula basada en la altura, podemos obtener resultados precisos.

Cómo calcular el área del triángulo escaleno

Para calcular el área de un triángulo escaleno, primero debemos determinar la longitud de sus lados. Esto se puede lograr midiendo directamente cada uno de ellos o utilizando información proporcionada en un problema o ejercicio específico.

Una vez que tenemos las longitudes de los lados, procedemos a calcular la altura del triángulo. La altura es una línea perpendicular trazada desde uno de los vértices del triángulo hasta la base o uno de los lados. Dependiendo de la información que tengamos disponible, podemos utilizar diferentes métodos para determinar la altura:

• Método del área: si conocemos el área del triángulo y la longitud de la base, podemos utilizar la fórmula del área de un triángulo (Área = (base * altura) / 2) para despejar la altura.
• Método de los lados: si conocemos las longitudes de los tres lados, podemos utilizar la fórmula de Herón para calcular el área y la fórmula de la altura en términos de los lados.
• Método de Pitágoras: si conocemos las longitudes de dos lados y el ángulo entre ellos, podemos usar el teorema de Pitágoras para encontrar la longitud de la altura.

Una vez que tenemos la altura del triángulo, simplemente multiplicamos la longitud de la base por la altura y dividimos el resultado entre 2. Esto nos dará el área del triángulo escaleno.

Ejemplo práctico

Supongamos que tenemos un triángulo escaleno con una base de 8 cm y una altura de 6 cm. Para calcular su área, multiplicamos la longitud de la base por la altura y dividimos el resultado entre 2:

Área = (8 cm * 6 cm) / 2 = 24 cm²

Por lo tanto, el área de este triángulo escaleno es de 24 centímetros cuadrados.

Calcular el área del triángulo escaleno puede parecer un proceso complicado debido a la falta de una fórmula general, pero con los métodos adecuados y la información necesaria, es posible obtener resultados precisos de manera sencilla. Esta habilidad es fundamental en diversos campos y puede ser de gran utilidad en situaciones prácticas o académicas.

Existen diferentes métodos para calcular el área de un triángulo escaleno

es y al menos una longitud de lado del triángulo.

Utilizando la fórmula Área = (lado1 * lado2 * seno(angulo)) / 2, donde "lado1" y "lado2" son las longitudes de dos lados del triángulo y "angulo" es el valor del ángulo opuesto a esos dos lados, se puede calcular el área del triángulo escaleno.

En resumen, existen diferentes métodos para calcular el área de un triángulo escaleno, como la fórmula de Herón, la fórmula de base por altura y utilizando medidas de ángulos. Estas fórmulas permiten obtener resultados precisos y variados según la información disponible.

Cómo puedo verificar si mi cálculo del área fue correcto

Una vez que hayas realizado el cálculo del área del triángulo escaleno de forma sencilla y precisa, es importante verificar si tus resultados son correctos. Esto puede ayudarte a tener confianza en tu trabajo y también te permite detectar posibles errores o inexactitudes en el proceso.

Para verificar si tu cálculo del área fue correcto, puedes seguir estos pasos:

1. Comprueba tus medidas

Es fundamental asegurarte de haber medido correctamente los lados del triángulo. Verifica que hayas tomado las medidas adecuadas para la base y la altura del triángulo, así como para los lados.

Utiliza una regla o un instrumento de medición preciso para obtener resultados más exactos. Si tus medidas no son precisas, es probable que tu cálculo del área tampoco lo sea.

2. Realiza los cálculos nuevamente

Siempre es recomendable repetir los cálculos para confirmar tus resultados. Revisa cada paso y asegúrate de no haber cometido errores matemáticos o de haber omitido alguna operación.

Puedes utilizar diferentes métodos para calcular el área del triángulo escaleno, como la fórmula básica o la fórmula de Herón. Asegúrate de elegir el método correcto según las medidas que hayas obtenido.

3. Utiliza herramientas online o aplicaciones móviles

Si aún tienes dudas sobre tus resultados, puedes utilizar herramientas online o aplicaciones móviles especializadas en el cálculo del área de triángulos. Estas herramientas suelen ser muy precisas y te permiten verificar tus resultados de manera rápida y sencilla.

Simplemente ingresa las medidas correspondientes y la herramienta calculará el área del triángulo escaleno por ti. Compara los resultados obtenidos con tus propios cálculos y verifica si coinciden.

4. Consulta fuentes confiables o un experto en matemáticas

Si después de haber realizado todos los pasos anteriores aún tienes dudas sobre tus resultados, siempre es recomendable consultar fuentes confiables o a un experto en matemáticas. Puedes buscar información en libros, sitios web académicos o incluso hacerle preguntas a profesores o personas especializadas en el tema.

Ellos podrán revisar tus cálculos y brindarte su opinión profesional para confirmar si tu cálculo del área del triángulo escaleno fue correcto.

Recuerda que la verificación de tu cálculo del área del triángulo escaleno es fundamental para tener confianza en tus resultados y asegurarte de que no has cometido errores. Siguiendo estos pasos, podrás confirmar la precisión de tus cálculos y tener una mayor seguridad en tu trabajo matemático.

Hay alguna fórmula adicional que se pueda utilizar para calcular el área del triángulo escaleno

Calcular el área de un triángulo escaleno puede parecer complicado debido a la falta de lados y ángulos iguales, pero no te preocupes, hay una fórmula que puedes utilizar para obtener un resultado preciso.

La fórmula del área de un triángulo escaleno se basa en la longitud de sus lados. Para calcular el área, necesitarás conocer la longitud de al menos uno de los lados y la altura correspondiente a ese lado. Afortunadamente, existen diferentes métodos que puedes utilizar para encontrar estos valores.

Método 1: Utilizando la fórmula general del área del triángulo

La fórmula general del área de un triángulo es:

Área = (base * altura) / 2

Para aplicar esta fórmula al triángulo escaleno, deberás seguir los siguientes pasos:

1. Elige uno de los lados del triángulo y su altura correspondiente. La altura puede ser trazada perpendicularmente desde el vértice opuesto al lado elegido.
2. Calcula el área utilizando la fórmula general del triángulo, donde la base es la longitud del lado elegido y la altura es la altura correspondiente.

Por ejemplo, si conoces que el lado del triángulo mide 5 unidades y su altura correspondiente es de 4 unidades, puedes aplicar la fórmula de la siguiente manera:

Área = (5 * 4) / 2 = 10 unidades cuadradas

De esta manera, utilizando la fórmula general del área del triángulo, puedes calcular el área de un triángulo escaleno sin problemas.

Método 2: Utilizando la fórmula de Herón

Otra forma de calcular el área de un triángulo escaleno es utilizando la fórmula de Herón. Esta fórmula se basa en los lados del triángulo y no requiere conocer la altura. La fórmula es:

Área = √(s * (s - a) * (s - b) * (s - c))

Donde s representa el semiperímetro del triángulo y se calcula sumando la longitud de los tres lados y dividiendo el resultado entre 2. Además, a, b y c son las longitudes de los lados del triángulo.

Para aplicar esta fórmula, deberás seguir estos pasos:

1. Calcula el semiperímetro sumando la longitud de los tres lados y dividiendo el resultado entre 2.
2. Utiliza la fórmula de Herón para calcular el área del triángulo usando el semiperímetro y las longitudes de los lados.

Por ejemplo, si los lados del triángulo miden 6 unidades, 8 unidades y 10 unidades, puedes aplicar la fórmula de Herón de la siguiente manera:

Primero, calcula el semiperímetro:

s = (6 + 8 + 10) / 2 = 12 unidades

Luego, utiliza la fórmula de Herón para calcular el área:

Área = √(12 * (12 - 6) * (12 - 8) * (12 - 10)) = √(12 * 6 * 4 * 2) = √(576) = 24 unidades cuadradas

De este modo, utilizando la fórmula de Herón podrás obtener el área de un triángulo escaleno sin necesidad de conocer la altura.

Ahora que conoces estas dos fórmulas, puedes calcular fácilmente el área de un triángulo escaleno. Recuerda que es importante utilizar los valores correctos y realizar los cálculos de manera precisa para obtener resultados precisos.

Qué aplicaciones prácticas tiene el conocer el área del triángulo escaleno

El cálculo del área del triángulo escaleno es una habilidad fundamental en matemáticas y geometría. Aunque pueda parecer un concepto abstracto, conocer el área de un triángulo escaleno tiene aplicaciones prácticas en diversas áreas de la vida cotidiana.

Una de las aplicaciones más comunes está en el ámbito de la construcción y la arquitectura. Los triángulos escalenos son utilizados en el diseño de estructuras y edificaciones, ya que ofrecen una mayor versatilidad que los triángulos equiláteros o isósceles. Al conocer el área de un triángulo escaleno, los arquitectos pueden calcular con precisión la cantidad de materiales necesarios para construir una estructura determinada, como por ejemplo, la cantidad de pintura necesaria para cubrir una fachada o la cantidad de revestimiento cerámico para un piso.

Otra aplicación práctica se encuentra en la cartografía y la topografía. Los profesionales que se dedican a estas disciplinas utilizan triángulos escalenos para medir distancias y realizar mediciones exactas de terrenos y mapas. Al calcular el área de un triángulo escaleno presente en un mapa, los cartógrafos y topógrafos pueden determinar la extensión de un territorio o la ubicación precisa de un punto geográfico.

Además, el conocimiento del área del triángulo escaleno es útil en campos como la ingeniería civil, la navegación y la física. En la ingeniería civil, por ejemplo, los ingenieros utilizan el área de los triángulos escalenos para calcular la resistencia de materiales o dimensionar correctamente una estructura. En navegación, el cálculo del área del triángulo escaleno es esencial para determinar la posición exacta de un barco en el mar utilizando el método de triangulación. Y en física, el área de un triángulo escaleno puede ayudar a calcular la magnitud de fuerzas o la superficie de contacto entre objetos en interacción.

El cálculo del área del triángulo escaleno es una habilidad matemática con múltiples aplicaciones prácticas en diversos campos, desde la construcción y la arquitectura hasta la cartografía y la ingeniería. Conocer el área de un triángulo escaleno nos permite realizar mediciones precisas, dimensionar estructuras, determinar posiciones geográficas y analizar fuerzas y superficies de contacto, entre otras muchas aplicaciones. Sin lugar a dudas, dominar este concepto geométrico nos brinda herramientas fundamentales para comprender y solucionar problemas del mundo real.

Existen otros conceptos relacionados que debería aprender sobre el triángulo escaleno

Además del cálculo del área, existen otros conceptos relacionados que es importante conocer sobre el triángulo escaleno. Estos conceptos permiten comprender mejor las características y propiedades de este tipo de triángulos, lo cual puede resultar útil en diversas aplicaciones matemáticas y en la vida cotidiana.

1. Perímetro del triángulo escaleno

El perímetro de un triángulo escaleno se refiere a la suma de las longitudes de sus tres lados. Para calcular el perímetro, es necesario conocer las medidas de los tres lados del triángulo. Una vez que se tienen estas medidas, simplemente se suman para obtener el resultado deseado. Es importante tener en cuenta que debido a que el triángulo escaleno no tiene lados iguales, el perímetro será diferente en cada caso.

2. Altura del triángulo escaleno

La altura de un triángulo escaleno se refiere a la distancia perpendicular desde uno de sus vértices a la base opuesta (que puede ser cualquiera de los tres lados). Calcular la altura de un triángulo escaleno puede ser un poco más complicado que en otros tipos de triángulos, ya que no se trata de un triángulo rectángulo donde la altura se encuentra dentro del triángulo formando un ángulo recto.

Existen diferentes métodos para calcular la altura de un triángulo escaleno, como por ejemplo utilizando la fórmula del área y la longitud de la base. Otra opción es utilizar la fórmula de la distancia entre un punto y una recta, donde el punto sería un vértice del triángulo y la recta sería el lado opuesto.

3. Congruencia de triángulos escalenos

La congruencia entre dos triángulos se refiere a que ambos tienen los mismos ángulos y longitudes de lados, aunque puedan estar en diferente posición o tamaño. En el caso de los triángulos escalenos, también es posible hablar de congruencia, pero existen más combinaciones posibles que en triángulos isósceles o equiláteros.

Para determinar si dos triángulos escalenos son congruentes, es necesario comparar los ángulos y las longitudes de los lados. Si los ángulos de ambos triángulos son iguales y las longitudes de los lados correspondientes también lo son, entonces se puede afirmar que los triángulos son congruentes.

4. Relación con otros polígonos

Los triángulos escalenos no son los únicos polígonos que existen en la geometría. Existen muchos otros polígonos regulares e irregulares que se pueden estudiar y comparar con respecto a sus características y propiedades.

Por ejemplo, uno de los polígonos más conocidos es el cuadrado, el cual tiene cuatro lados iguales y cuatro ángulos rectos. Comparado con un triángulo escaleno, el cuadrado presenta diferencias significativas en cuanto a su forma, por lo que sus propiedades y cálculos son distintos.

Es importante explorar la relación que existe entre los triángulos escalenos y otros polígonos, ya que esto proporciona una visión más amplia de la geometría y ayuda a desarrollar habilidades matemáticas.

• Conocer el perímetro, altura, congruencia y relación con otros polígonos son algunos conceptos relacionados que se deben aprender sobre el triángulo escaleno. Estos conocimientos no solo sirven para comprender mejor este tipo de triángulos, sino que también son fundamentales en la resolución de problemas geométricos y aplicaciones prácticas.

1. ¿Cuál es la fórmula para calcular el área de un triángulo escaleno? La fórmula del área del triángulo escaleno es: A = (base * altura) / 2.

2. ¿Qué datos necesito conocer para poder calcular el área de un triángulo escaleno? Para calcular el área de un triángulo escaleno, debes conocer la medida de la base y la altura.

3. ¿Cómo encuentro la base de un triángulo escaleno si no me la dan en el problema? Si no te proporcionan la medida de la base, puedes utilizar la fórmula del perímetro del triángulo para calcularla sumando las medidas de los otros dos lados y restándolas a la medida total del perímetro.

4. ¿Puedo utilizar otra fórmula para calcular el área de un triángulo escaleno? Sí, además de la fórmula mencionada anteriormente, también puedes utilizar la fórmula de Herón si conoces las medidas de los tres lados del triángulo.

5. ¿Existe alguna regla especial para calcular el área de un triángulo escaleno con ángulos obtusos? No existe una regla especial para calcular el área de un triángulo escaleno con ángulos obtusos. Puedes utilizar la fórmula tradicional mencionada en la pregunta 1.