Binomio al Cuadrado: Descubre el Método Infalible para Resolverlo en Pocos Pasos

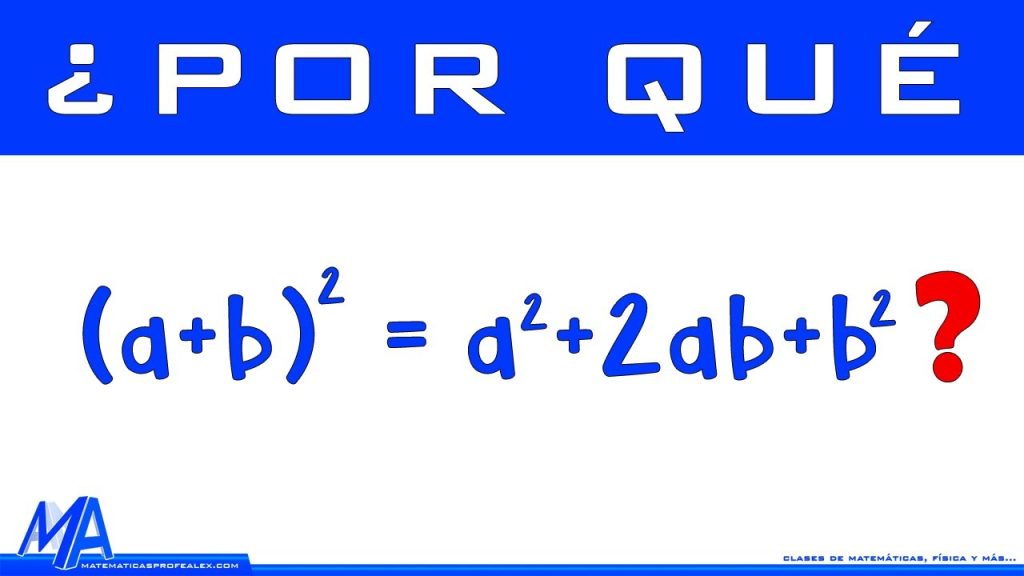
El binomio al cuadrado es un problema comúnmente abordado en matemáticas, especialmente en álgebra. Se trata de una operación que implica elevar al cuadrado a un binomio, es decir, multiplicar dicho binomio por sí mismo. Este concepto es fundamental para expandir expresiones algebraicas y resolver ecuaciones.

Aprenderás el método infalible para resolver el binomio al cuadrado en pocos pasos. Nos enfocaremos en explicar de manera clara y concisa cómo aplicar este proceso, utilizando ejemplos prácticos que te ayudarán a comprender mejor el contenido. Además, te daremos algunos tips y trucos para facilitar tu comprensión y aplicación de esta técnica matemática.

Qué es un binomio al cuadrado y por qué es importante

Un binomio al cuadrado es una expresión algebraica que resulta de elevar al cuadrado un binomio. Un binomio es una suma o resta de dos términos algebraicos, y al elevarlo al cuadrado obtenemos una expresión más compleja.

Resolver binomios al cuadrado es una habilidad fundamental en álgebra, ya que aparece con frecuencia en diferentes contextos matemáticos. Comprender cómo resolver binomios al cuadrado nos permite simplificar ecuaciones, factorizar polinomios y encontrar soluciones a problemas prácticos en diversas áreas como la física, la economía y la estadística.

Cómo resolver un binomio al cuadrado

Para resolver un binomio al cuadrado, podemos utilizar el método FOIL (First, Outer, Inner, Last), que consiste en distribuir los términos del binomio original de la siguiente manera:

(a + b)^2 = a^2 + 2ab + b^2

Donde "a" y "b" son los términos del binomio original. El primer término del resultado es el cuadrado del primer término del binomio original, el segundo término es el doble del producto de ambos términos del binomio original, y el tercer término es el cuadrado del segundo término del binomio original.

Veamos un ejemplo para entender mejor este proceso:

(2x + 3)^2 = (2x)^2 + 2(2x)(3) + (3)^2

Simplificando esta expresión:

4x^2 + 12x + 9

Por lo tanto, el binomio al cuadrado (2x + 3)^2 se resuelve como 4x^2 + 12x + 9.

Es importante notar que el método FOIL es utilizado específicamente para resolver binomios al cuadrado. Para elevar al cuadrado expresiones más complejas, es necesario aplicar otros métodos como la regla del polinomio cuadrado perfecto o la regla del trinomio cuadrado perfecto.

Aplicaciones de los binomios al cuadrado

Los binomios al cuadrado tienen múltiples aplicaciones en matemáticas y otras disciplinas. Algunas de las principales aplicaciones incluyen:

• Ecuaciones cuadráticas: Las ecuaciones cuadráticas son aquellas en las que una variable está elevada al cuadrado. Resolver estas ecuaciones implica frecuentemente trabajar con binomios al cuadrado.
• Factorización de polinomios: Los binomios al cuadrado ayudan a factorizar polinomios, es decir, descomponer una expresión en sus factores primos. Esta habilidad es esencial para simplificar expresiones y resolver problemas matemáticos.
• Método de completar el cuadrado: Al resolver ecuaciones cuadráticas, el método de completar el cuadrado utiliza el concepto de binomio al cuadrado para llevar la ecuación a una forma más fácil de resolver.

Los binomios al cuadrado son herramientas matemáticas poderosas que nos permiten resolver ecuaciones algebraicas y simplificar expresiones. A través del método FOIL, podemos resolver binomios al cuadrado en pocos pasos, facilitando nuestra comprensión y aplicación de conceptos algebraicos más avanzados.

Cuál es el método infalible para resolver un binomio al cuadrado

El binomio al cuadrado es una expresión algebraica que se caracteriza por tener dos términos elevados al cuadrado y un producto de ambos términos. Resolver un binomio al cuadrado puede parecer complicado a primera vista, pero con el método infalible que te presentaremos a continuación, podrás resolverlo en pocos pasos de manera sencilla y efectiva.

Paso 1: Identificar los términos y sus coeficientes

Antes de empezar, es importante identificar los términos del binomio y sus respectivos coeficientes. Un binomio está compuesto por dos términos separados por un signo más (+) o menos (-). Cada uno de estos términos tiene su propio coeficiente numérico que lo acompaña. Es fundamental tener claridad sobre estos elementos para seguir adelante con el proceso de resolución.

Paso 2: Aplicar la regla del cuadrado de un binomio

El siguiente paso consiste en aplicar la regla del cuadrado de un binomio, que establece que:

(a + b)^2 = a^2 + 2ab + b^2

En esta fórmula, "a" y "b" representan los términos que componen el binomio al cuadrado. Siguiendo esta regla, elevamos cada término al cuadrado y obtenemos los productos correspondientes. Luego, sumamos todos los términos obtenidos para obtener el resultado final.

Paso 3: Simplificar y simplificar nuevamente

Una vez aplicada la regla del cuadrado de un binomio, podemos simplificar la expresión resultante. Esto implica combinar términos que sean semejantes y eliminar cualquier término nulo.

Es importante tener en cuenta que a veces resulta necesario repetir este paso varias veces hasta obtener una expresión completamente simplificada. No te preocupes si esto sucede, ya que forma parte del proceso y ayuda a asegurar la corrección de los resultados obtenidos.

Paso 4: Verificar el resultado

Después de haber simplificado la expresión obtenida, es fundamental verificar el resultado para asegurarnos de que sea correcto. Para ello, podemos realizar diversas comprobaciones, como volver a expandir la expresión simplificada y compararla con la expresión original. Si ambas expresiones son equivalentes, habremos resuelto correctamente el binomio al cuadrado.

Resolver un binomio al cuadrado puede ser un proceso sencillo si se sigue el método infalible que hemos descrito. Identificar los términos y sus coeficientes, aplicar la regla del cuadrado de un binomio, simplificar la expresión y verificar el resultado son los pasos clave para resolver este tipo de ejercicios de manera eficiente y exitosa.

Recuerda practicar y poner en práctica estos pasos con diferentes ejemplos de binomios al cuadrado para fortalecer tus habilidades en álgebra y resolver estos problemas de forma rápida y precisa.

Cuáles son los pasos para resolver un binomio al cuadrado

Resolver un binomio al cuadrado puede parecer complicado al principio, pero en realidad es un proceso bastante sencillo si se siguen los pasos adecuados. A continuación te explicaré cómo resolver un binomio al cuadrado de manera infalible en pocos pasos.

Paso 1: Identificar el tipo de binomio

Antes de comenzar con la resolución del binomio al cuadrado, es importante identificar el tipo de binomio con el que estamos trabajando. Los binomios pueden ser de diferentes tipos, como por ejemplo: binomio conjugado, binomio con término común o binomio especial. Dependiendo del tipo de binomio, utilizaremos distintas estrategias para su resolución.

Paso 2: Aplicar la fórmula del binomio al cuadrado

Una vez identificado el tipo de binomio, procedemos a aplicar la fórmula del binomio al cuadrado. La fórmula general para resolver un binomio al cuadrado es:

(a + b)^2 = a^2 + 2ab + b^2

Donde a y b son los términos del binomio.

Paso 3: Simplificar las operaciones

Una vez aplicada la fórmula, debemos simplificar las operaciones matemáticas realizadas en cada uno de los términos del binomio al cuadrado. Esto implica realizar las multiplicaciones y sumas correspondientes siguiendo las reglas básicas de la aritmética.

Paso 4: Simplificar términos semejantes

En algunos casos, es posible que aparezcan términos semejantes en la expresión. Si esto ocurre, debemos simplificar dichos términos mediante las operaciones correspondientes. Esto implica sumar o restar coeficientes iguales y mantener la misma variable elevada al mismo exponente.

Paso 5: Verificar el resultado final

Una vez simplificados los términos del binomio al cuadrado, es importante verificar el resultado obtenido. Para ello, podemos realizar ciertos cálculos adicionales o simplemente despejar las variables en caso de ser necesario para asegurarnos de que no haya errores en nuestra resolución.

Resolver un binomio al cuadrado puede ser un proceso sencillo si se siguen los pasos adecuados. Identificar el tipo de binomio, aplicar la fórmula correspondiente, simplificar las operaciones y términos, y verificar el resultado final son pasos clave para resolver cualquier binomio al cuadrado de manera infalible en pocos pasos.

Cómo se simplifica un binomio al cuadrado

El binomio al cuadrado es una expresión algebraica que se obtiene al multiplicar un binomio por sí mismo. Resolverlo puede parecer complicado, pero en realidad existe un método infalible para simplificarlo en pocos pasos.

Paso 1: Identificar el binomio

Lo primero que debemos hacer es identificar el binomio que vamos a elevar al cuadrado. Un binomio está conformado por dos términos separados por un signo de suma o resta. Por ejemplo, si tenemos el binomio (a + b), ese será nuestro binomio base.

Paso 2: Multiplicación del binomio consigo mismo

Ahora procedemos a multiplicar el binomio por sí mismo. Para hacer esto, utilizamos la propiedad distributiva y combinamos cada término del primer binomio con los términos del segundo binomio. Siguiendo el ejemplo anterior, tendríamos:

(a + b) * (a + b)

Aplicando la propiedad distributiva, obtenemos:

a * a + a * b + b * a + b * b

Simplificando cada uno de los productos, llegamos a:

a^2 + ab + ba + b^2

Ten en cuenta que el producto de un término consigo mismo resulta en su exponente al cuadrado.

Paso 3: Ordenamiento y simplificación de términos

Para simplificar aún más la expresión, agrupamos los términos semejantes y los ordenamos de mayor a menor exponente. En este caso, podemos agrupar los términos "ab" y "ba", ya que son equivalentes. Así llegamos a:

a^2 + 2ab + b^2

Finalmente, hemos simplificado el binomio al cuadrado en una expresión mucho más manejable.

Ejemplo de aplicación del método

Para ilustrar cómo funciona el método, consideremos el binomio (x + 3). Al elevarlo al cuadrado, seguimos los pasos anteriores:

1. Multiplicación del binomio consigo mismo: (x + 3) * (x + 3)
2. Aplicación de la propiedad distributiva: x * x + x * 3 + 3 * x + 3 * 3
3. Simplificación de términos: x^2 + 3x + 3x + 9
4. Ordenamiento y simplificación de términos: x^2 + 6x + 9

Por lo tanto, el binomio (x + 3) elevado al cuadrado se puede simplificar como x^2 + 6x + 9.

Ahora que conoces el método infalible para resolver un binomio al cuadrado, podrás simplificar expresiones algebraicas con mayor facilidad. Recuerda practicar con diferentes ejemplos para afianzar tu comprensión y resolver problemas más complejos.

Qué herramientas matemáticas se utilizan para resolver un binomio al cuadrado

Resolver un binomio al cuadrado es una técnica matemática que se utiliza para simplificar y factorizar expresiones algebraicas. Para llevar a cabo este proceso, se requiere el conocimiento y uso de diferentes herramientas matemáticas, las cuales nos ayudarán a llegar al resultado final de manera precisa y efectiva.

Multplicación de polinomios

Una de las herramientas indispensables para resolver un binomio al cuadrado es la multiplicación de polinomios. Esta operación consiste en combinar los términos de dos expresiones algebraicas mediante la distribución, es decir, multiplicando cada término del primer polinomio por cada término del segundo polinomio.

Por ejemplo, si tenemos el binomio (a + b), para resolverlo al cuadrado debemos multiplicar cada término dentro del paréntesis por sí mismo: (a + b)(a + b). Aplicando la distribución, obtenemos: a * a + a * b + b * a + b * b. Simplificando, tenemos: a^2 + 2ab + b^2.

Identidades algebraicas

Otra herramienta fundamental para resolver un binomio al cuadrado son las identidades algebraicas. Estas son fórmulas matemáticas que nos permiten simplificar expresiones y encontrar patrones en los resultados.

La identidad algebraica más utilizada para resolver un binomio al cuadrado es la siguiente: (a + b)^2 = a^2 + 2ab + b^2. Esta fórmula nos indica que al elevar un binomio a la potencia de dos, el resultado se obtiene sumando el cuadrado del primer término, el doble producto del primer y segundo término, y el cuadrado del segundo término.

Fórmula general

Además de las herramientas mencionadas anteriormente, también podemos utilizar la fórmula general para resolver un binomio al cuadrado. Esta fórmula nos facilita el cálculo del resultado final sin necesidad de realizar multiplicaciones o aplicar identidades algebraicas.

La fórmula general para resolver un binomio al cuadrado es la siguiente: (a + b)^2 = a^2 + 2ab + b^2. Al sustituir los valores de a y b en la fórmula, obtenemos directamente el resultado final sin necesidad de realizar operaciones adicionales.

Es importante señalar que estas herramientas matemáticas son solo algunas de las utilizadas para resolver un binomio al cuadrado. Dependiendo de la complejidad de la expresión algebraica, pueden requerirse otros métodos y técnicas específicas.

• Multiplicación de polinomios
• Identidades algebraicas
• Fórmula general

Para resolver un binomio al cuadrado se utilizan diferentes herramientas matemáticas como la multiplicación de polinomios, las identidades algebraicas y la fórmula general. Estas herramientas nos permiten simplificar y factorizar las expresiones algebraicas de manera eficiente y precisa, facilitando así la resolución de problemas matemáticos relacionados con binomios al cuadrado.

Existen casos especiales en los que el método infalible no funciona? ¿Cómo manejarlos

El método infalible para resolver un binomio al cuadrado es una herramienta extremadamente útil, pero es importante tener en cuenta que existen casos especiales en los que este método no funciona de manera directa. Sin embargo, no hay razón para entrar en pánico, ya que existen algunas estrategias que podemos utilizar para manejar estos casos de manera efectiva.

Uno de los casos más comunes es cuando el binomio al cuadrado presenta coeficientes diferentes. En estos casos, es necesario realizar ciertas operaciones antes de aplicar el método infalible. Primero, identificamos si podemos factorizar alguno de los coeficientes con el fin de obtener un factor común. Si esto es posible, lo factorizamos y luego procedemos a aplicar el método infalible al binomio resultante.

Otro caso especial se da cuando el binomio al cuadrado contiene términos de diferente signo. Para solucionar esto, debemos trabajar con la propiedad distributiva y utilizar las reglas de los signos. Específicamente, multiplicamos cada término del binomio por sí mismo y nos aseguramos de aplicar correctamente los signos correspondientes a cada uno. Al realizar esta operación, obtendremos un nuevo binomio al cuadrado en el cual todos los términos tendrán el mismo signo, lo cual nos permitirá aplicar el método infalible sin problemas.

Por último, otro caso especial se presenta cuando el binomio al cuadrado contiene términos irracionales o radicales. En estos casos, es recomendable utilizar las propiedades de las raíces cuadradas para simplificar la expresión. Podemos descomponer cada término en su forma más sencilla y luego aplicar el método infalible al binomio resultante. En ocasiones, también podemos recurrir a técnicas de aproximación o redondeo para obtener un resultado estimado.

Aunque el método infalible para resolver un binomio al cuadrado es muy eficiente, existen casos especiales que requieren de una estrategia adicional. La clave está en identificar las características particulares de cada binomio y utilizar las herramientas matemáticas adecuadas para manejar estas situaciones. Con práctica y perseverancia, podremos resolver cualquier binomio al cuadrado, incluso aquellos que parecen desafiantes a primera vista.

Cuáles son las aplicaciones prácticas de resolver binomios al cuadrado

Resolver binomios al cuadrado es una habilidad matemática fundamental que tiene aplicaciones prácticas en diversos campos. Este método infalible nos permite simplificar expresiones algebraicas y resolver ecuaciones de manera más eficiente.

Una de las principales aplicaciones de resolver binomios al cuadrado se encuentra en la factorización de expresiones algebraicas. Al utilizar este método, podemos descomponer una expresión en factores que nos permiten simplificarla y entender mejor su estructura. Esto es especialmente útil en la resolución de ecuaciones cuadráticas, donde podemos representar una ecuación de segundo grado como el producto de dos binomios al cuadrado.

Otra aplicación práctica es en la resolución de problemas relacionados con áreas y volúmenes. El binomio al cuadrado nos permite encontrar fácilmente el área de un cuadrado o el volumen de un cubo, por ejemplo. Además, puede ser utilizado para calcular áreas y volúmenes de formas más complejas, como los cubos perfectos, donde se necesita conocer la fórmula del binomio al cuadrado para obtener el resultado preciso.

Ejemplo de aplicación práctica: Resolución de una ecuación cuadrática

Imagina que tienes una ecuación cuadrática de la forma x^2 + 4x + 4 = 0. Para resolver esta ecuación, podemos utilizar el método del binomio al cuadrado para simplificarla.

Primero, identificamos que el coeficiente principal es 1 (el número que acompaña a x^2). Luego, dividimos el coeficiente lineal (el número que acompaña a x) en dos partes iguales y las elevamos al cuadrado. En este caso, obtenemos el término (2)^2 = 4.

Ahora, reescribimos la ecuación original utilizando el binomio al cuadrado: (x + 2)^2 = 0. Esta nueva expresión nos permite identificar de manera clara que el resultado es igual a cero.

Finalmente, resolvemos la ecuación tomando la raíz cuadrada en ambos lados: x + 2 = 0. Despejando la incógnita, obtendremos la solución final: x = -2.

Como podemos observar, el método del binomio al cuadrado nos permitió simplificar la ecuación cuadrática y resolverla de manera más rápida y eficiente. Esta aplicación práctica demuestra la importancia de dominar esta técnica matemática para abordar problemas más complejos en distintas áreas.

Cuál es la importancia de dominar la resolución de binomios al cuadrado en álgebra

La resolución de binomios al cuadrado es una habilidad fundamental en el campo del álgebra. Al dominar esta técnica, los estudiantes adquieren una base sólida para abordar conceptos más avanzados en esta rama de las matemáticas.

Los binomios son expresiones algebraicas compuestas por dos términos separados por un signo de suma o resta. Al elevarlos al cuadrado, se obtiene un polinomio con tres términos, siendo el primero y el último cuadrados perfectos y el término del medio el doble del producto de ambos términos originales.

¿Por qué es importante aprender a resolver binomios al cuadrado?

Una de las principales razones por las que es crucial dominar la resolución de binomios al cuadrado es que esta técnica se utiliza ampliamente en muchas áreas de las matemáticas y la física. Desde ecuaciones cuadráticas hasta fórmulas de geometría, los binomios al cuadrado aparecen en numerosos problemas y situaciones que los estudiantes deben enfrentar.

Además, la resolución de binomios al cuadrado es un paso fundamental para comprender y aplicar el teorema del binomio, que es una herramienta poderosa para expandir expresiones y simplificar cálculos.

Otro motivo por el cual es importante dominar la resolución de binomios al cuadrado es que esta habilidad desarrolla el pensamiento lógico y analítico de los estudiantes. Al enfrentarse a un problema de este tipo, deben identificar patrones, aplicar reglas matemáticas y realizar operaciones algebraicas para llegar a una solución precisa.

Finalmente, el dominio de la resolución de binomios al cuadrado brinda a los estudiantes la confianza necesaria para abordar problemas más complejos en el álgebra. Al tener un entendimiento sólido de esta técnica, se sienten más cómodos al enfrentarse a desafíos matemáticos y son capaces de aplicarla de manera efectiva en diversos contextos.

Explorando el método infalible para resolver binomios al cuadrado

Aunque resolver binomios al cuadrado puede parecer intimidante al principio, existe un método infalible que sigue una serie de pasos claros y concisos.

1. Paso 1: Identificar los términos iniciales del binomio al cuadrado.
2. Paso 2: Elevar cada uno de estos términos al cuadrado.
3. Paso 3: Multiplicar el primer término al cuadrado por el segundo término al cuadrado.
4. Paso 4: Escribir el polinomio resultante colocando el término del paso 3 en el medio y los términos al cuadrado del paso 2 como primero y último.

Este método proporciona una guía clara y sistemática para resolver cualquier binomio al cuadrado, lo que facilita su aplicación y asegura resultados precisos.

Dominar la resolución de binomios al cuadrado es de vital importancia para los estudiantes de álgebra. No solo les brinda las herramientas necesarias para enfrentar problemas matemáticos más avanzados, sino que también desarrolla su pensamiento lógico y analítico. Al aplicar el método infalible para resolver binomios al cuadrado, los estudiantes adquieren una base sólida en esta técnica y se sienten más confiados al abordar desafíos algebraicos.

Cómo puedo practicar y mejorar mis habilidades en la resolución de binomios al cuadrado

Resolver binomios al cuadrado puede parecer un desafío al principio, pero con la práctica y el uso de un método infalible, podrás mejorar tus habilidades y resolverlos en pocos pasos. En este artículo, aprenderás cómo practicar y perfeccionar tus técnicas para la resolución de estos problemas matemáticos.

1. Comprende los conceptos básicos

Antes de comenzar a resolver binomios al cuadrado, es fundamental que comprendas los conceptos básicos involucrados en este tipo de operaciones. Un binomio al cuadrado es una expresión algebraica que se obtiene al elevar al cuadrado un binomio. Un binomio está compuesto por dos términos separados por un signo más o menos. Por ejemplo, (a + b) es un binomio.

2. Conoce el método FOIL

El método FOIL es una técnica muy útil para multiplicar binomios y, posteriormente, resolverlos al cuadrado. La palabra FOIL es un acrónimo de las palabras: First, Outer, Inner, and Last. Estos corresponden a los pasos que debemos seguir para multiplicar los términos de dos binomios. Siguiendo la secuencia FOIL, comenzamos multiplicando el primer término de cada binomio, luego los términos externos, después los internos y finalmente los últimos términos. Asegúrate de familiarizarte con este método y practicar su aplicación en diferentes ejemplos.

3. Practica con ejercicios

La práctica constante es clave para mejorar tus habilidades en la resolución de binomios al cuadrado. Busca ejercicios que te permitan aplicar el método FOIL y resolverlos paso a paso. Comienza con ejercicios más simples y gradualmente ve aumentando su nivel de dificultad. Con cada ejercicio que resuelvas, estarás fortaleciendo tus conocimientos y agilizando tu proceso de resolución.

4. Utiliza recursos en línea

Existen numerosos recursos en línea que pueden ayudarte a practicar y mejorar tus habilidades en la resolución de binomios al cuadrado. Puedes encontrar problemas propuestos, tutoriales en video, ejercicios interactivos y mucho más. Aprovecha estos recursos para ampliar tus conocimientos y desarrollar una mayor confianza en tus habilidades matemáticas.

5. Identifica patrones y estrategias

A medida que vayas resolviendo diferentes ejercicios de binomios al cuadrado, intenta identificar patrones o estrategias que te ayuden a resolverlos más rápidamente. Por ejemplo, puedes descubrir que ciertos términos se anulan entre sí o que algunos productos son fácilmente simplificables. Estas observaciones te permitirán resolver los binomios al cuadrado de manera más eficiente y eficaz.

6. Aplica el método infalible

Una vez que hayas dominado el método FOIL y hayas practicado lo suficiente, podrás utilizar el método infalible para resolver binomios al cuadrado en pocos pasos. Este método consiste en aplicar el método FOIL para multiplicar los términos del binomio, y luego, simplificar la expresión resultante. Recuerda que siempre debes seguir una secuencia lógica y ordenada al resolver estos problemas.

Para concluir, mejorar tus habilidades en la resolución de binomios al cuadrado requiere práctica y conocimiento de los conceptos básicos. Utiliza el método FOIL como base para entrenarte y practicar con una amplia variedad de ejercicios. Aprovecha los recursos en línea y busca patrones y estrategias que te ayuden a resolverlos más rápidamente. Con dedicación y perseverancia, pronto te convertirás en un experto en la resolución de binomios al cuadrado.

Dónde puedo encontrar ejercicios y recursos adicionales para aprender más sobre binomios al cuadrado

Si estás interesado en aprender más sobre binomios al cuadrado y quieres practicar con ejercicios adicionales, estás en el lugar correcto. Aquí te proporcionaremos algunos recursos y recomendaciones para que puedas seguir profundizando en este tema.

Páginas web especializadas

Existen varias páginas web especializadas en matemáticas que ofrecen una amplia gama de ejercicios y problemas relacionados con los binomios al cuadrado. Algunas de estas páginas incluyen:

• EjerciciosMatematicas.com: Esta página ofrece una sección dedicada exclusivamente a los binomios al cuadrado, donde encontrarás ejercicios clasificados por nivel de dificultad. Además, también cuentan con explicaciones detalladas paso a paso para que puedas comprender adecuadamente cada ejercicio.
• MatesFacil.com: En esta página podrás acceder a una gran cantidad de ejercicios interactivos sobre binomios al cuadrado. La plataforma te brinda la posibilidad de resolver los ejercicios directamente en la página y obtener retroalimentación inmediata.
• MatematicasParaTodos.net: Esta página ofrece una amplia variedad de recursos educativos, incluyendo ejercicios resueltos y propuestos sobre binomios al cuadrado. Además, también encontrarás videos explicativos que te ayudarán a comprender mejor los conceptos.

Libros de texto

Otra opción para encontrar ejercicios y recursos adicionales es consultar libros de texto especializados en álgebra o matemáticas avanzadas. Algunos libros recomendados que tratan este tema incluyen:

1. Álgebra Lineal: Una Introducción Moderna, de David Poole.
2. Álgebra y Trigonometría, de Michael Sullivan.
3. Análisis Matemático I, de Eduardo Espinoza Ramos.

Estos libros brindan una explicación detallada sobre los binomios al cuadrado, así como una amplia variedad de ejercicios resueltos y propuestos para practicar.

Aplicaciones móviles

Si prefieres la comodidad de tu dispositivo móvil, existen varias aplicaciones que te permiten practicar binomios al cuadrado en cualquier momento y lugar. Algunas de las aplicaciones más populares incluyen:

• Mathway: Esta aplicación no solo te permite resolver ejercicios de binomios al cuadrado, sino también otros problemas matemáticos complejos. Solo tienes que ingresar el ejercicio y la aplicación te mostrará la solución paso a paso.
• Photomath: Con esta aplicación, puedes tomar una foto del ejercicio y la aplicación te dará la respuesta correcta, pero también te mostrará el proceso paso a paso para que puedas aprender cómo resolverlo tú mismo.
• Wolfram Alpha: Esta aplicación es una herramienta poderosa que puede resolver una amplia variedad de problemas matemáticos, incluyendo binomios al cuadrado. Solo tienes que ingresar el problema y la aplicación te dará la solución detallada.

Estas son solo algunas de las opciones disponibles para encontrar ejercicios y recursos adicionales sobre binomios al cuadrado. Recuerda que la práctica constante es clave para mejorar tus habilidades matemáticas, por lo que te recomendamos que dediques tiempo a resolver diferentes tipos de ejercicios y problemas.

Preguntas frecuentes (FAQ)

1. ¿Cuál es la fórmula para resolver un binomio al cuadrado?

La fórmula para resolver un binomio al cuadrado es (a + b)^2 = a^2 + 2ab + b^2.

2. ¿Cómo se aplica el método del binomio al cuadrado?

Para aplicar el método del binomio al cuadrado, se deben identificar los valores de "a" y "b", luego se eleva cada término al cuadrado y finalmente se suman los resultados.

3. ¿Qué significa expandir un binomio al cuadrado?

Expandir un binomio al cuadrado significa multiplicar el binomio por sí mismo, es decir, realizar todas las combinaciones posibles de multiplicaciones entre los términos del binomio.

4. ¿Qué es el término "trinomio cuadrado perfecto"?

Un trinomio cuadrado perfecto es aquel que se obtiene al elevar al cuadrado un binomio de la forma (a + b) o (a - b).

5. ¿Se puede aplicar el método del binomio al cuadrado a más de dos términos?

No, el método del binomio al cuadrado solo se aplica a binomios, es decir, expresiones algebraicas con dos términos separados por un signo de suma o resta.