Arista de un cubo: 5 claves fundamentales para entender su significado y utilidad

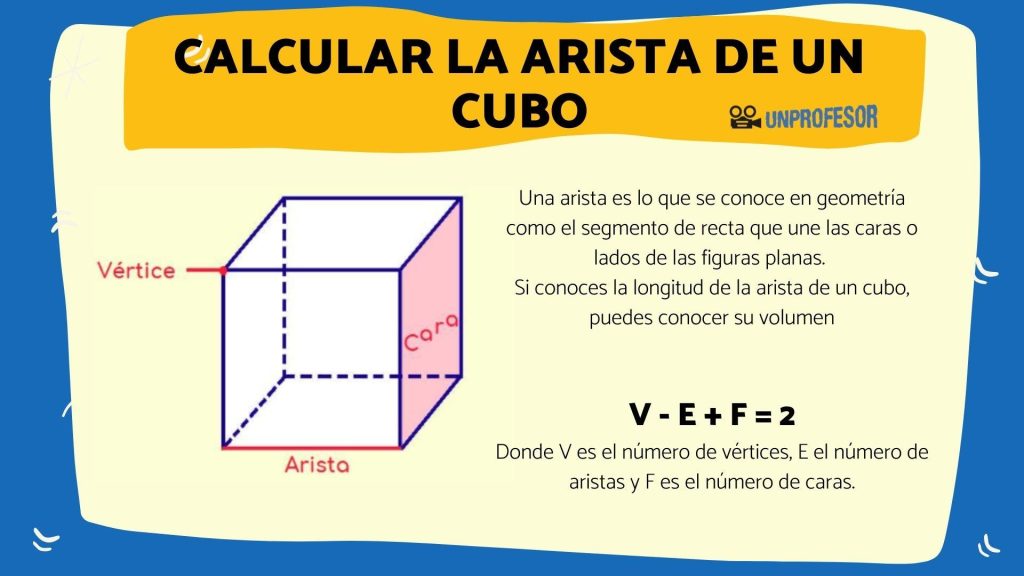
La arista de un cubo es uno de los conceptos fundamentales en la geometría tridimensional. Se trata de las líneas rectas que se forman en la intersección de dos caras del cubo. Las aristas determinan la forma y estructura del cubo, y son clave para entender sus propiedades y aplicaciones en diversos campos.

En este artículo vamos a explorar cinco claves fundamentales para entender el significado y utilidad de las aristas en un cubo. Explicaremos qué son las aristas, cómo se calculan, su relación con las caras y los vértices del cubo, y cómo se utilizan en diferentes áreas como la arquitectura, el diseño gráfico y la programación 3D. Además, también discutiremos algunos ejemplos prácticos que ilustran la importancia de las aristas en la vida cotidiana.

Qué es una arista en un cubo y cómo se define

Una arista en un cubo es uno de los elementos fundamentales que conforman su estructura. Se trata de una línea recta que conecta dos vértices del cubo, formando uno de los bordes o caras de la figura geométrica tridimensional.

De manera más precisa, cada arista está compuesta por dos segmentos de recta iguales y paralelos entre sí, cuyos extremos coinciden con dos vértices del cubo. Estas líneas rectas están situadas de manera perpendicular a las caras adyacentes del cubo, lo que les confiere estabilidad y rigidez a la estructura.

La definición formal de una arista en un cubo se puede expresar como la intersección de dos planos perpendiculares, donde cada plano coincide con una de las caras del cubo. Cabe mencionar que, debido a su naturaleza tridimensional, un cubo tiene un total de doce aristas.

Características principales de las aristas en un cubo

• Longitud: Todas las aristas de un cubo tienen la misma longitud, ya que están formadas por segmentos de recta iguales.
• Simetría: Cada arista presenta una simetría respecto al centro del cubo, es decir, es posible encontrar otra arista de igual longitud y posición relativa respecto a los vértices.
• Conexión: Las aristas permiten la conexión entre los vértices del cubo, facilitando la formación de las distintas caras y solidificando la estructura del sólido geométrico.
• Perpendicularidad: Las aristas están dispuestas de manera perpendicular a las caras adyacentes del cubo, lo que confiere estabilidad y rigidez a su estructura.
• Intersecciones: Cada arista se cruza con otras tres aristas en los vértices del cubo, formando una intersección característica.

Utilidad de las aristas en un cubo

Las aristas en un cubo son fundamentales para comprender y representar la forma y la estructura de esta figura geométrica tridimensional. Su presencia permite visualizar las relaciones espaciales entre los vértices y las caras del cubo, así como establecer la conexión entre ellos.

Además, las aristas desempeñan un papel crucial en diversas áreas del conocimiento, como la geometría, la arquitectura, la ingeniería y el diseño gráfico. En geometría, por ejemplo, las aristas son utilizadas para calcular el perímetro y el área de una cara del cubo, así como para determinar otros elementos relacionados con la figura.

En el ámbito de la arquitectura y la ingeniería, las aristas en un cubo son consideradas en el diseño y la construcción de estructuras sólidas, donde su disposición y conexión influyen en la resistencia y estabilidad de dichas construcciones. De igual manera, en el diseño gráfico, las aristas son representadas de manera simbólica para crear la ilusión de formas tridimensionales en imágenes y representaciones visuales.

Comprender el significado y la utilidad de las aristas en un cubo es esencial para entender y trabajar con figuras geométricas tridimensionales, así como para aplicar su conocimiento en distintas disciplinas y áreas del saber humano.

Cuántas aristas tiene un cubo

El cubo, también conocido como hexaedro, es uno de los sólidos platónicos más reconocidos dentro de la geometría tridimensional. Se trata de un poliedro regular compuesto por seis caras cuadradas congruentes, doce aristas y ocho vértices.

En cuanto a las aristas, son aquellos segmentos de línea que conectan dos vértices consecutivos en una figura geométrica. Cada cara del cubo está delimitada por cuatro aristas, siendo entonces un total de 12 aristas en un cubo.

Es importante destacar que todas las aristas del cubo tienen la misma longitud, ya que todas las caras son cuadradas y congruentes entre sí. Esta característica proporciona al cubo una estructura simétrica y equilibrada en sus dimensiones.

La cantidad de aristas en un cubo es fundamental para entender su significado y utilidad en diferentes áreas del conocimiento, como la arquitectura, la ingeniería, la física y las matemáticas. A continuación, te presentamos cinco claves principales para comprender su importancia:

1. Elemento estructural básico

El cubo es considerado uno de los elementos estructurales básicos en la arquitectura y la ingeniería civil. Su forma cúbica y sus aristas rectas lo convierten en un componente ideal para construir edificaciones, puentes y otras estructuras. La estabilidad y resistencia que ofrece el cubo gracias a sus aristas contribuyen a soportar cargas y distribuir adecuadamente los esfuerzos.

2. Representación del espacio tridimensional

El cubo es un sólido tridimensional que nos permite representar visualmente el espacio en tres dimensiones. Sus aristas rectas y congruentes proporcionan una percepción clara de las distancias en los ejes cartesianos (x, y, z) y permiten comprender mejor la ubicación relativa de objetos en un entorno tridimensional.

3. Simbolismo matemático

En el ámbito matemático, el cubo y sus aristas tienen un significado simbólico importante. La potenciación al cubo -elevar un número a la tercera potencia- se representa con el símbolo ^3 y está relacionada directamente con un cubo geométrico. Esta operación matemática es fundamental en cálculos y en diversas aplicaciones científicas.

4. Volumen y área superficial

Las aristas de un cubo no solo determinan su forma, sino también sus medidas dentro del espacio tridimensional. El volumen se calcula multiplicando la longitud de una arista por sí misma tres veces (a^3), mientras que el área superficial se obtiene multiplicando la longitud de una arista por seis (6a^2), ya que el cubo tiene seis caras congruentes.

5. Concepto de cubicidad

La cubicidad es un término utilizado en diversos campos para describir la relación entre el volumen y la superficie de un objeto. En el caso del cubo, su forma cúbica garantiza una alta cubicidad, lo que indica que posee un volumen relativamente grande en comparación con su área superficial. Esta propiedad lo convierte en un elemento eficiente para almacenar y transportar líquidos o sólidos, e incluso es empleado en la industria para calcular métricas de eficiencia en procesos de producción.

Cuál es el significado de las aristas en un cubo

Las aristas en un cubo son los segmentos de línea que conectan dos vértices del cubo. Son las líneas que forman los bordes del cubo y le dan una forma estructurada y definida. Cada cubo tiene un total de 12 aristas.

El significado de las aristas en un cubo va más allá de ser simplemente líneas visibles en su estructura. Estas aristas son esenciales para comprender y describir las propiedades geométricas de un cubo, así como para entender sus aplicaciones prácticas en diversas áreas.

Clave 1: Delimitación y definición

Las aristas cumplen un papel fundamental en la delimitación y definición de un cubo. Gracias a ellas, es posible visualizar claramente los distintos planos y caras que componen al cubo. Además, permiten establecer las distancias y relaciones entre los vértices y las caras del cubo. Sin las aristas, el cubo perdería su forma distintiva y no podríamos entender su estructura tridimensional.

Clave 2: Identificación de vértices

Las aristas facilitan también la identificación de los vértices en un cubo. Cada arista conecta dos vértices, lo que nos permite reconocer y ubicar cada uno de ellos en relación al resto de la estructura del cubo. Con las aristas como guía, podemos distinguir claramente los ocho vértices del cubo y comprender cómo se interconectan entre sí.

Clave 3: Medición de distancias

Otra utilidad importante de las aristas en un cubo es la posibilidad de medir distancias entre los vértices. Al ser segmentos de línea, nos proporcionan una referencia visual y numérica para determinar la longitud de cada arista y calcular distancias dentro del cubo. Esta capacidad de medición resulta especialmente valiosa en campos como la arquitectura, donde se requiere precisión en las dimensiones y espacios.

Clave 4: Visualización de planos y caras

Cuando observamos un cubo, las aristas también nos permiten visualizar con claridad los distintos planos y caras que lo conforman. Cada arista define el límite entre dos caras adyacentes, lo que nos ayuda a comprender cómo se organiza la superficie del cubo. De esta manera, las aristas contribuyen a la representación y comprensión de la geometría en tres dimensiones.

Clave 5: Intersección y relación de aristas

Las aristas no existen de manera aislada en un cubo, sino que se intersecan y se relacionan entre sí. Esta intersección de las aristas permite establecer ángulos y formas geométricas adicionales en el cubo. El estudio de estas intersecciones es fundamental para entender patrones y propiedades matemáticas en la geometría del cubo.

Las aristas son elementos clave en la comprensión y análisis de un cubo. No solo definen su estructura tridimensional, sino que también nos brindan información sobre la ubicación de los vértices, las distancias, los planos y las intersecciones. La importancia de las aristas en un cubo trasciende su apariencia visual y juega un papel fundamental en diversos campos como la geometría, la arquitectura y otras disciplinas que requieren una comprensión profunda de las formas tridimensionales.

Cuál es la utilidad de conocer las aristas en un cubo

Las aristas en un cubo son elementos fundamentales para comprender su estructura y utilidad. Estas líneas rectas que conectan los vértices del cubo son la base sobre la cual se construye su forma geométrica característica.

La principal utilidad de conocer las aristas en un cubo reside en la capacidad de poder determinar la longitud de cada uno de los lados de esta figura tridimensional. Al medir la longitud de una arista, podemos obtener información precisa sobre las dimensiones del cubo, lo que resulta especialmente útil en diversos campos como la arquitectura, la ingeniería o las ciencias físicas.

1. Cálculo del perímetro de un cubo

Una de las claves más importantes al entender las aristas de un cubo es su relación con el cálculo del perímetro. El perímetro de un cubo se obtiene sumando las longitudes de sus cuatro aristas laterales. Conocer las medidas de estas aristas nos permite calcular el perímetro total del cubo, lo que resulta esencial en áreas como la construcción o la carpintería, donde se requiere conocer con precisión las dimensiones exteriores de una estructura.

2. Identificación de caras adyacentes

Otra clave fundamental al comprender las aristas en un cubo es su conexión directa con la identificación de caras adyacentes. Las aristas nos permiten determinar qué caras están unidas entre sí en esta figura tridimensional. Al seguir las aristas, podemos visualizar las caras adyacentes y comprender cómo se relacionan entre sí, lo que resulta útil en el estudio de la geometría y la topología.

3. Manejo de la simetría del cubo

Las aristas también desempeñan un papel importante en el manejo de la simetría del cubo. Al seguir las aristas, podemos identificar los ejes de simetría y los puntos de reflexión en esta figura geométrica. Esta información es valiosa en campos como el arte y el diseño, donde la simetría se utiliza con frecuencia para crear composiciones equilibradas y estéticamente agradables.

4. Determinación de diagonales en un cubo

Las aristas en un cubo también nos permiten determinar las diagonales en esta figura geométrica. Al unir los vértices no adyacentes a través de las aristas, obtenemos las diagonales del cubo. Identificar y comprender estas diagonales es esencial en problemas de trigonometría y cálculo vectorial, donde se requiere conocer las distancias y direcciones en el espacio tridimensional.

5. Visualización espacial y percepción de dimensiones

Por último, el conocimiento de las aristas de un cubo contribuye a desarrollar habilidades de visualización espacial y percepción de dimensiones. Al estudiar y comprender cómo las aristas conectan los vértices del cubo, nuestra capacidad para imaginar y manipular objetos tridimensionales mejora significativamente. Esta habilidad es fundamental en áreas como la física y la matemática, donde se trabaja constantemente con conceptos y modelos en tres dimensiones.

Conocer las aristas en un cubo es fundamental para comprender su significado y utilidad. Desde el cálculo del perímetro y la identificación de caras adyacentes, hasta el manejo de la simetría y la determinación de diagonales, las aristas brindan información clave en diversos campos académicos y profesionales. Además, el conocimiento de las aristas contribuye a desarrollar habilidades de visualización espacial y percepción de dimensiones, lo que nos ayuda a comprender mejor el mundo tridimensional que nos rodea.

Cómo se calcula la longitud de las aristas en un cubo

La longitud de las aristas en un cubo es fundamental para entender y caracterizar este sólido geométrico tridimensional. En términos simples, una arista se define como la línea recta que conecta dos vértices consecutivos en un cubo. Para calcular la longitud de las aristas en un cubo, se requiere conocer algunas propiedades básicas y utilizar fórmulas matemáticas específicas.

1. Identificación de los vértices del cubo

Antes de empezar a calcular la longitud de las aristas, es importante identificar y ubicar los vértices del cubo. Un cubo tiene ocho vértices en total, y cada uno de ellos representa el punto de encuentro de tres aristas distintas. Al reconocer y marcar los vértices correctamente, se facilita el proceso de cálculo de las aristas.

2. Características de las aristas en un cubo

Las aristas en un cubo presentan algunas características clave que permiten comprender su naturaleza y utilidad en el contexto de la geometría. En primer lugar, todas las aristas de un cubo son congruentes entre sí, lo que significa que tienen la misma longitud. Además, todas las aristas son perpendiculares entre sí y forman ángulos rectos en su intersección. Estas características hacen que las aristas sean elementos fundamentales para determinar la forma y estructura del cubo.

3. Fórmula para calcular la longitud de las aristas

Para calcular la longitud de las aristas en un cubo, se utiliza la fórmula siguiente:

Longitud de las aristas = Volumen / Área de una cara

Donde el volumen se calcula elevando al cubo la longitud de una arista y el área de una cara se obtiene multiplicando la longitud de una arista por sí misma.

4. Ejemplo práctico de cálculo de las aristas en un cubo

• Supongamos que tenemos un cubo con un volumen de 125 cm³.
• Para determinar la longitud de las aristas en el cubo, aplicamos la fórmula:

Longitud de las aristas = ³√(Volumen) / √(Área de una cara)

Sustituyendo los valores conocidos:

Longitud de las aristas = ³√(125 cm³) / √(Área de una cara)

Despejando el valor del área de una cara:

Área de una cara = (Longitud de las aristas)²

Luego, sustituyendo nuevamente los valores conocidos:

Área de una cara = (Longitud de las aristas)² = (Longitud de las aristas) * (Longitud de las aristas)

Finalmente, despejando el valor de la longitud de las aristas:

Longitud de las aristas = ³√(125 cm³) / √{}

Mediante el uso de esta fórmula y los valores adecuados, se puede calcular la longitud de las aristas en cualquier cubo dado su volumen.

5. Aplicaciones de la longitud de las aristas en el mundo real

La longitud de las aristas en un cubo tiene diversas aplicaciones prácticas en el mundo real, especialmente en campos como la ingeniería, la física y la arquitectura. Por ejemplo, en la construcción de estructuras tridimensionales, conocer la longitud de las aristas de un cubo es esencial para garantizar la estabilidad y resistencia de la edificación. Del mismo modo, en la física, la longitud de las aristas puede ser utilizada para calcular otras propiedades del cubo, como su volumen o su área superficial.

Preguntas frecuentes (FAQ)

1. ¿Qué es una arista de un cubo?

Una arista de un cubo es un segmento de línea que une dos vértices del cubo.

2. ¿Cuántas aristas tiene un cubo?

Un cubo tiene 12 aristas en total.

3. ¿Cómo se calcula la longitud de las aristas de un cubo?

La longitud de las aristas de un cubo se calcula multiplicando la longitud de una arista por 12.

4. ¿Cuál es la función de las aristas en un cubo?

Las aristas en un cubo ayudan a definir su forma y estructura, así como a determinar las relaciones espaciales entre sus distintos elementos.

5. ¿Cómo se diferencian las aristas en un cubo de otras figuras geométricas?

Las aristas en un cubo se caracterizan por ser líneas rectas de igual longitud que conectan vértices adyacentes, mientras que en otras figuras se pueden encontrar aristas curvas o de diferentes longitudes.