7 sencillos pasos para calcular la apotema de un hexágono y dominar la geometría

La geometría es una rama de las matemáticas que estudia las propiedades y las medidas de las figuras en el espacio. Uno de los conceptos más fundamentales en geometría es la apotema, que es la distancia entre el centro de una figura regular y uno de sus lados. Calcular la apotema de un hexágono puede ser un desafío para muchos estudiantes, pero con unos simples pasos se puede dominar este concepto y ampliar el conocimiento en geometría.

Te mostraremos 7 sencillos pasos para calcular la apotema de un hexágono de forma clara y concisa. Primero, repasaremos los conceptos básicos sobre los hexágonos y las propiedades que los caracterizan. Luego, explicaremos cada paso detalladamente, desde cómo encontrar el área del hexágono hasta cómo utilizar esa información para calcular la apotema. Con esta guía práctica, podrás resolver cualquier ejercicio relacionado a la apotema de un hexágono sin mayor dificultad.

Qué es la apotema de un hexágono y por qué es importante conocerla

La apotema de un hexágono es una medida que nos permite determinar la distancia desde el centro del hexágono hasta cualquiera de sus lados. Es una herramienta fundamental en el campo de la geometría, ya que nos brinda información esencial para el cálculo de áreas, volúmenes y otros aspectos relacionados con esta figura geométrica.

Conocer la apotema de un hexágono es especialmente importante cuando trabajamos con construcciones arquitectónicas, diseño gráfico o cualquier otra disciplina que requiera un conocimiento preciso de las formas y dimensiones.

Calcular la apotema de un hexágono puede parecer complejo al principio, pero siguiendo los siguientes pasos te resultará sencillo y podrás dominar la geometría en poco tiempo:

Paso 1: Conoce las características básicas del hexágono

Antes de calcular la apotema, es importante que comprendas las propiedades fundamentales de un hexágono. Un hexágono es un polígono con seis lados y seis ángulos. Todos sus lados tienen la misma longitud y sus ángulos internos miden 120 grados.

Paso 2: Identifica las medidas necesarias

Para calcular la apotema de un hexágono, necesitarás conocer la medida de uno de sus lados. Si no tienes esta medida, deberás medirlo utilizando una regla, una cinta métrica u otro instrumento adecuado.

Paso 3: Utiliza la fórmula para calcular la apotema

La fórmula para calcular la apotema de un hexágono es:

apotema = lado / (2 * tangente(180° / número de lados))

Paso 4: Convierte los ángulos a radianes

Ten en cuenta que en la fórmula se utiliza la función tangente, la cual requiere que los ángulos estén expresados en radianes. Para convertir los ángulos de grados a radianes, utiliza la siguiente fórmula:

radianes = grados * π / 180°

Paso 5: Reemplaza los valores en la fórmula

Una vez que has convertido los ángulos a radianes, puedes reemplazar los valores correspondientes en la fórmula para calcular la apotema. Recuerda utilizar la medida del lado que obteniste en el paso 2 y el número de lados del hexágono.

Paso 6: Realiza las operaciones matemáticas

Realiza las operaciones matemáticas indicadas en la fórmula para obtener el valor de la apotema del hexágono. Si lo deseas, utiliza una calculadora para facilitar el cálculo.

Paso 7: Verifica y redondea el resultado

Una vez que hayas realizado todas las operaciones, verifica el resultado final. Es posible que obtengas un valor con decimales; en ese caso, redondea a la cantidad de decimales adecuada según tus necesidades o requerimientos.

¡Y eso es todo! Ahora ya sabes cómo calcular la apotema de un hexágono. Recuerda practicar con diferentes ejemplos para afianzar tus conocimientos y dominar la geometría. Esta habilidad te será útil en diversas aplicaciones, así que ¡a ponerla en práctica!

Cuáles son las fórmulas para calcular la apotema de un hexágono regular e irregular

La geometría es una rama de las matemáticas que se encarga del estudio de las formas, las figuras y sus propiedades. Dentro de esta área, el cálculo de la apotema es de gran importancia y se utiliza en diferentes ámbitos como la arquitectura, la ingeniería y la carpintería. En este artículo, te guiaremos a través de los pasos necesarios para calcular la apotema de un hexágono, tanto en su forma regular como en su forma irregular.

¿Qué es un hexágono?

Antes de adentrarnos en cómo se calcula la apotema de un hexágono, es importante entender qué es un hexágono. Un hexágono es una figura plana que consta de seis lados y seis ángulos. Los hexágonos pueden tener lados de igual longitud, lo que los convierte en hexágonos regulares, o pueden tener lados de diferentes longitudes, lo que los convierte en hexágonos irregulares.

¿Qué es la apotema de un hexágono?

La apotema de un hexágono es la distancia más corta desde el centro del hexágono hasta cualquiera de sus lados. En otras palabras, es la distancia entre el centro del hexágono y uno de sus vértices. La apotema se representa con la letra "a". Calcular la apotema es útil para determinar el área de un hexágono y también puede ser utilizada en la construcción de estructuras geométricas.

Fórmulas para calcular la apotema de un hexágono regular e irregular

Tanto en un hexágono regular como en uno irregular, existen fórmulas diferentes para calcular la apotema. A continuación, te mostraremos ambas:

1. Hexágono regular:

La fórmula para encontrar la apotema de un hexágono regular es:

a = l / (2 * tan(π / 6))

Donde "a" representa la apotema y "l" representa la longitud de uno de los lados del hexágono.

2. Hexágono irregular:

En el caso de un hexágono irregular, no existe una fórmula única para encontrar la apotema. Sin embargo, una aproximación puede ser:

a ≈ (A1 + A2 + A3 + A4 + A5 + A6) / 6

Donde "A1", "A2", "A3", "A4", "A5" y "A6" representan las áreas de los triángulos formados por los lados del hexágono y su apotema.

Es importante tener en cuenta que estas fórmulas son aplicables únicamente a hexágonos regulares e irregulares convexos, es decir, aquellos cuyos ángulos internos son menores a 180 grados. En casos de hexágonos cóncavos, la apotema puede ser más difícil de calcular y requeriría un enfoque diferente.

El cálculo de la apotema de un hexágono es fundamental para determinar su área y puede ser útil en diversos campos. Tanto en un hexágono regular como en uno irregular, existen fórmulas específicas que permiten encontrar la apotema. Esperamos que este artículo te haya sido de utilidad y te invite a adentrarte aún más en el fascinante mundo de la geometría.

Cuál es la relación entre el radio y la apotema de un hexágono regular

Para comprender la relación entre el radio y la apotema de un hexágono regular, es importante tener en cuenta las características básicas de esta figura geométrica. Un hexágono regular es un polígono de seis lados iguales y seis ángulos internos también iguales. Además, todos sus lados son tangentes a una circunferencia inscrita, es decir, una circunferencia que toca los puntos medios de cada uno de los lados del hexágono.

El radio de un hexágono regular es la distancia entre su centro y cualquiera de sus vértices. Por otro lado, la apotema es la distancia entre el centro del hexágono y el punto donde se intersectan dos lados opuestos. Es importante destacar que la apotema es perpendicular a los lados del hexágono y atraviesa su centro.

Ahora bien, ¿cuál es la relación entre el radio y la apotema de un hexágono regular? Podemos establecer que el radio es igual a la longitud de la apotema más la longitud de un lado del hexágono. Es decir:

Radio = Apotema + Lado

Esta relación se debe a que tomamos en consideración que desde el centro del hexágono hasta el punto de intersección de los lados opuestos existe una línea recta que forma un triángulo rectángulo con la apotema como hipotenusa y la mitad de un lado como cateto adyacente.

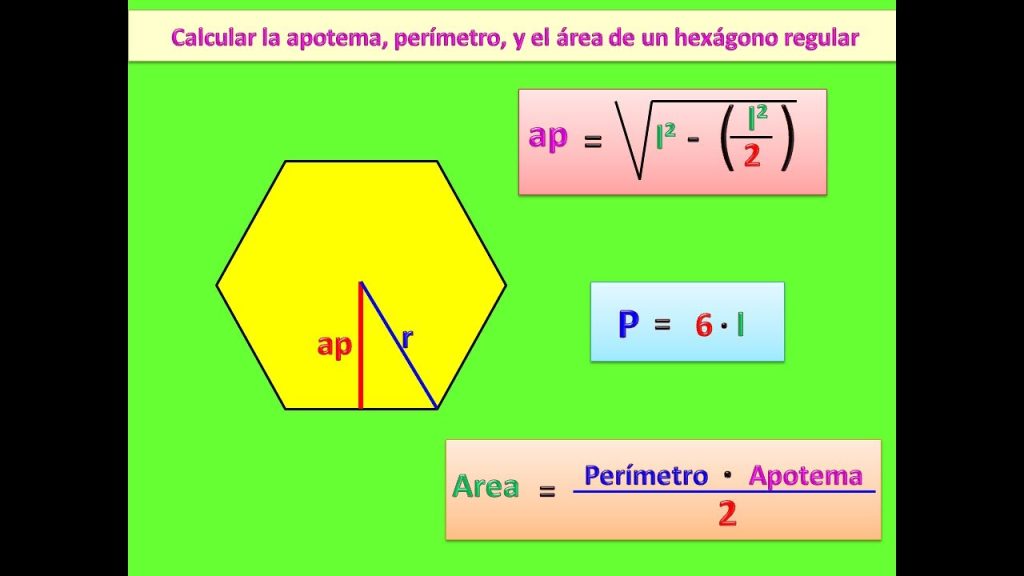
Es importante destacar que tanto el radio como la apotema son medidas fundamentales para calcular distintas propiedades y realizar diferentes cálculos relacionados con un hexágono regular. Uno de los cálculos más comunes es el área de un hexágono, que se puede obtener multiplicando la apotema por el perímetro del hexágono y dividiendo el resultado entre dos:

Área = (Apotema * Perímetro) / 2

La relación entre el radio y la apotema de un hexágono regular es que el radio está dado por la suma de la apotema y la longitud de uno de sus lados. Tanto el radio como la apotema son medidas fundamentales para cálculos relacionados con esta figura geométrica, como el área y otros cálculos específicos. Comprender esta relación nos permite dominar la geometría y utilizarla de manera efectiva en diferentes contextos.

Cuáles son los pasos para calcular la apotema de un hexágono regular

Calcular la apotema de un hexágono regular puede parecer complicado, pero siguiendo estos simples pasos te convertirás en un experto en geometría. La apotema es una línea que va desde el centro del hexágono hasta uno de sus lados, y es esencial para calcular su área y otros aspectos geométricos.

Paso 1: Conoce el largo de un lado

Antes de poder calcular la apotema, necesitas saber la medida de uno de los lados del hexágono regular. Puedes medirlo con una regla o utilizar las dimensiones proporcionadas si estás trabajando con una figura preexistente.

Paso 2: Encuentra el perímetro del hexágono

El perímetro de un hexágono regular se calcula multiplicando la longitud de uno de los lados por seis, ya que todos los lados son iguales en este tipo de figura geométrica. Por lo tanto, el perímetro (P) se obtiene de la siguiente manera: P = 6 × largo del lado.

Paso 3: Calcula el apotema utilizando la fórmula

La fórmula para calcular la apotema de un hexágono regular es: a = l / (2 × tan(π/6)), donde "a" representa la apotema y "l" es el largo de uno de los lados.

a = l / (2 × tan(π/6))

Paso 4: Convierte radianes a grados

En la fórmula anterior, se utiliza el ángulo π/6 expresado en radianes. Si deseas trabajar con grados, puedes usar la siguiente conversión: 1 radian (rad) = 180° / π ≈ 57.2957795°.

Paso 5: Sustituye los valores en la fórmula

Ahora que tienes todos los datos necesarios, sustituye el valor del largo del lado y realiza los cálculos. Recuerda utilizar los grados convertidos a radianes si estás trabajando con esta unidad angular.

Paso 6: Simplifica la expresión

Una vez realices los cálculos, puedes simplificar la expresión, si es necesario, para obtener un resultado más preciso y manejable.

Paso 7: Verifica el resultado

Finalmente, verifica tu resultado calculando nuevamente el perímetro del hexágono utilizando la apotema obtenida y asegurándote de que coincide con el valor esperado. Si los números no concuerdan, revisa los pasos anteriores para encontrar posibles errores.

Ahora que conoces los 7 pasos para calcular la apotema de un hexágono regular, ¡puedes aplicar este conocimiento en tus problemas de geometría y dominar esta área de las matemáticas con facilidad! Recuerda practicar para mejorar tus habilidades y pronto serás capaz de resolver cualquier problema relacionado con hexágonos y otras figuras geométricas.

Cómo se puede medir la apotema de un hexágono si no conocemos su radio

Calcular la apotema de un hexágono puede ser una tarea sencilla si conocemos su radio, pero ¿qué hacer cuando no disponemos de esa información? Afortunadamente, existen métodos alternativos que nos permiten obtener el valor de la apotema incluso sin conocer el radio.

Paso 1: Medir uno de los lados del hexágono

Lo primero que necesitamos es tener a nuestra disposición un hexágono cuyos lados se puedan medir con precisión. Para ello, utilizaremos una regla o una cinta métrica.

Paso 2: Determinar la longitud del lado

Una vez que tenemos el hexágono a nuestra disposición, debemos medir uno de sus lados para poder continuar con el cálculo de la apotema. Es importante asegurarse de que la medición sea precisa y lo más exacta posible.

Paso 3: Calcular el perímetro del hexágono

Una vez que tenemos la longitud de uno de los lados del hexágono, podemos calcular el perímetro del hexágono. Esto se logra multiplicando la longitud del lado por la cantidad de lados del hexágono, es decir, por 6.

Perímetro = Longitud del lado x 6

Paso 4: Obtener el apotema a partir del perímetro

Ahora que conocemos el perímetro del hexágono, podemos usar la fórmula para calcular el apotema. La fórmula establece que el apotema es igual al perímetro dividido por dos veces la tangente de 30 grados.

Apotema = Perímetro / (2 * tan(30°))

Paso 5: Convertir la medida del apotema

Es posible que al calcular el apotema obtengamos un valor en radianes en lugar de una medida lineal. Para obtener una medida lineal, podemos multiplicar el valor del apotema por la longitud del lado.

Medida Lineal del Apotema = Apotema x Longitud del lado

Paso 6: Redondear el resultado

Dependiendo de las necesidades y requerimientos del cálculo, es posible que necesitemos redondear el valor obtenido para el apotema. En ese caso, debemos aplicar las reglas de redondeo correspondientes para obtener un valor aproximado más útil.

Paso 7: Comprobar el resultado

Finalmente, es importante comprobar el resultado obtenido mediante métodos alternativos, como utilizar la fórmula del área del hexágono y compararlo con otros valores conocidos. Esto nos ayudará a verificar la precisión de nuestro cálculo y a garantizar que hemos obtenido la medida correcta para la apotema.

Calcular la apotema de un hexágono sin conocer su radio puede ser un desafío interesante en el ámbito de la geometría. Sin embargo, siguiendo estos sencillos pasos y aplicando las fórmulas correspondientes, podremos dominar este concepto y obtener resultados precisos. ¡Practica y experimenta con diferentes hexágonos para afianzar tus conocimientos y convertirte en un experto en geometría!

Cuál es la diferencia entre la apotema y el radio de un polígono regular

La geometría es una rama de las matemáticas que nos permite estudiar las propiedades y medidas de las figuras y los objetos en el espacio. En particular, cuando hablamos de polígonos regulares, dos términos importantes que debemos comprender son la apotema y el radio.

El radio de un polígono regular es la distancia desde el centro del polígono hasta cualquier vértice. Es importante destacar que en un polígono regular, todos los radios tienen la misma longitud.

Por otro lado, la apotema se refiere a la distancia desde el centro del polígono hasta el punto medio de cualquier lado. A diferencia del radio, la apotema puede variar en longitud dependiendo del número de lados del polígono.

Para visualizar la diferencia entre la apotema y el radio, podemos imaginar un hexágono regular. En este caso, si trazamos el radio desde el centro del hexágono hasta uno de los vértices, obtendremos la longitud del radio. Sin embargo, si trazamos la apotema desde el centro hasta el punto medio de uno de los lados, obtendremos la longitud de la apotema.

La principal diferencia entre la apotema y el radio de un polígono regular radica en el punto hasta donde llega cada medida desde el centro de la figura. El radio llega hasta los vértices, mientras que la apotema llega hasta los puntos medios de los lados.

Cómo se aplica el cálculo de la apotema a otros polígonos regulares

El cálculo de la apotema es una herramienta fundamental en el campo de la geometría, que nos permite determinar la distancia desde el centro de un polígono regular hasta cualquiera de sus lados. Si bien hablamos específicamente del hexágono, este concepto se puede aplicar a otros polígonos regulares con igual facilidad.

Paso 1: Identificar el tipo de polígono

Antes de comenzar a calcular la apotema, es importante identificar el tipo de polígono con el que estamos trabajando. En nuestro caso, hablaremos de hexágonos, que son polígonos de seis lados iguales.

Paso 2: Conocer la longitud del lado

Para poder calcular correctamente la apotema, necesitamos conocer la longitud del lado del polígono regular. En el caso de un hexágono, es fundamental conocer esta medida antes de continuar.

Paso 3: Calcular el valor del ángulo central

Otro aspecto relevante para el cálculo de la apotema es el valor del ángulo central del polígono. Para esto, podemos usar la fórmula:

Ángulo central = 360° / número de lados

En el caso del hexágono, el ángulo central será de 60°.

Paso 4: Aplicar la función trigonométrica

La función trigonométrica que utilizaremos para calcular la apotema es la tangente, que se define como:

Tangente = Cateto opuesto / Cateto adyacente

En este caso, el cateto opuesto será la distancia entre el centro del polígono y uno de sus lados, es decir, la apotema. El cateto adyacente será la mitad de la longitud de un lado.

Paso 5: Calcular la medida de la apotema

Una vez que tenemos la función trigonométrica y los valores necesarios, podemos calcular la apotema utilizando la fórmula:

Apotema = Tangente * Cateto adyacente

De esta manera, encontraremos la medida exacta de la apotema del hexágono.

Paso 6: Aplicar a otros polígonos regulares

Como mencionamos al principio, este proceso se puede aplicar a otros polígonos regulares de manera similar. Los pasos dependerán de las características específicas de cada polígono, pero la idea básica será la misma: utilizar la función trigonométrica adecuada para encontrar la apotema.

Paso 7: Dominar la geometría y sus aplicaciones

Calcular la apotema de un polígono regular es solo uno de los muchos conceptos que se pueden explorar en el fascinante mundo de la geometría. Una vez que dominemos este cálculo, podremos expandir nuestro conocimiento y aplicarlo a otras áreas de estudio, como la construcción, la física y la arquitectura. La geometría nos brinda una base sólida para entender las formas y estructuras que nos rodean, y el cálculo de la apotema es solo el comienzo.

Qué aplicaciones prácticas tiene el conocimiento de la apotema de un hexágono en la vida cotidiana

La geometría es una rama de las matemáticas que tiene muchas aplicaciones prácticas en nuestra vida cotidiana, aunque a veces no nos demos cuenta. Uno de los conceptos importantes en geometría es la apotema de un polígono, que es la distancia desde el centro del polígono hasta uno de sus lados.

En este artículo, nos enfocaremos en la apotema de un hexágono y te mostraremos 7 sencillos pasos para calcularla. Pero antes de entrar en detalles sobre cómo hacerlo, vamos a hablar un poco sobre algunas aplicaciones prácticas que tiene el conocimiento de la apotema de un hexágono.

Materiales de construcción

El cálculo de la apotema de un hexágono es esencial en la construcción de diversos elementos arquitectónicos, como por ejemplo, los azulejos. Los azulejos de forma hexagonal requieren un conocimiento preciso de la apotema para asegurar una instalación adecuada. Además, también se utiliza en la fabricación de mosaicos, donde la apotema determina la posición exacta de cada pieza dentro del diseño.

Trabajo con madera

Otra aplicación común es en el trabajo con madera, especialmente en la fabricación de muebles o estructuras diseñadas con paneles regulares hexagonales. El cálculo de la apotema permite determinar correctamente las medidas necesarias para cortar los paneles y ensamblarlos de manera precisa.

Cálculo de áreas

El cálculo de áreas también es una aplicación importante de la apotema de un hexágono. El área de un hexágono se puede calcular conociendo su apotema, la longitud de sus lados o su radio. Esto es útil en diversas áreas como la arquitectura, la ingeniería y la carpintería, donde es necesario determinar el área de una superficie para aplicar adecuadamente los materiales.

Estudios geográficos

En estudios geográficos y urbanísticos, el cálculo de la apotema de hexágonos regulares se utiliza en la delimitación y subdivisión de terrenos y parcelas. También es de utilidad en la planificación urbana, donde se pueden utilizar hexágonos para representar áreas específicas y calcular la distancia a través de la apotema entre esos puntos.

Aplicaciones en la naturaleza

No solo en la construcción y las ciencias aplicadas se encuentra el uso de la apotema de un hexágono, también podemos encontrar ejemplos en la naturaleza. Un ejemplo famoso son los panales de abejas, que están compuestos por celdas hexagonales, y conocer la apotema permite comprender mejor la estructura y organización de estos insectos.

Estas son solo algunas de las muchas aplicaciones prácticas que tiene el conocimiento de la apotema de un hexágono en la vida cotidiana. Ahora que hemos visto su importancia, vamos a pasar a los pasos para calcularla. ¡Sigue leyendo!

Cuál es la importancia de dominar el cálculo de la apotema en el estudio de la geometría

El cálculo de la apotema es fundamental en el estudio de la geometría, ya que nos permite conocer información relevante acerca de la figura en cuestión. En el caso del hexágono, conocer la apotema nos ayuda a determinar diversas propiedades y características del polígono regular.

La apotema de un hexágono es la distancia desde el centro del hexágono hasta cualquiera de sus lados. Es decir, es la distancia más corta entre el centro y uno de los lados del hexágono. Calcular la apotema de un hexágono puede ser algo complejo si no se cuenta con las herramientas adecuadas o si no se domina el concepto.

Paso 1: Conocer el valor de la longitud de un lado

Antes de calcular la apotema de un hexágono, es necesario conocer el valor de la longitud de uno de sus lados. Esta medida puede variar dependiendo del tamaño del hexágono en cuestión. Si no se tiene esta información, es importante medir cuidadosamente uno de los lados con una regla o una cinta métrica.

Paso 2: Aplicar la fórmula para calcular la apotema

Una vez que se conoce el valor de la longitud de un lado del hexágono, podemos aplicar la fórmula para calcular la apotema. La fórmula general para calcular la apotema de un hexágono regular es:

A = s/2 * √3

Donde A representa la apotema, s es la longitud de un lado del hexágono.

Es importante recordar que esta fórmula aplica únicamente para hexágonos regulares, es decir, aquellos que tienen todos sus lados y ángulos iguales.

Paso 3: Resolver la fórmula

Para calcular la apotema de un hexágono, sustituimos el valor de la longitud del lado de nuestro hexágono en la fórmula mencionada anteriormente. Realizamos los cálculos necesarios hasta obtener el resultado final de la apotema. Es importante ser preciso y cuidadoso al realizar estas operaciones matemáticas.

Paso 4: Verificar la apotema obtenida

Una vez que hemos obtenido el valor numérico de la apotema, es recomendable verificar nuestra respuesta. Podemos utilizar diferentes métodos para confirmar si el cálculo ha sido realizado correctamente. Por ejemplo, podemos utilizar una regla o una cinta métrica para medir la apotema en el hexágono y compararla con el valor obtenido a través de nuestros cálculos matemáticos.

Paso 5: Utilizar la apotema en cálculos posteriores

Una vez que tenemos el valor de la apotema de nuestro hexágono, podemos utilizarlo en diferentes cálculos geométricos o aplicaciones prácticas. Por ejemplo, podemos utilizar la apotema junto con la fórmula del área para determinar el área de nuestro hexágono. También podemos utilizar la apotema para calcular el perímetro, la altura, o cualquier otra característica geométrica relacionada con el polígono.

Paso 6: Practicar y consolidar el conocimiento

El cálculo de la apotema puede resultar desafiante al principio, especialmente si estamos empezando a familiarizarnos con la geometría. Sin embargo, como en cualquier otro campo del conocimiento, la práctica constante es fundamental para dominar esta habilidad matemática. Es recomendable realizar ejercicios adicionales para seguir afianzando nuestros conocimientos sobre el tema y aumentar nuestra destreza en el cálculo de la apotema.

Paso 7: Aplicar el conocimiento a diferentes figuras geométricas

Aunque en este artículo nos hemos centrado en el cálculo de la apotema de un hexágono, es importante recordar que este concepto se aplica a una amplia variedad de figuras geométricas. La apotema es una medida clave en polígonos regulares como triángulos, cuadrados, pentágonos, heptágonos y muchos más. Al dominar el cálculo de la apotema en un hexágono, abrimos las puertas para comprender y resolver problemas de geometría relacionados con otras figuras poligonales.

El cálculo de la apotema en la geometría es una habilidad fundamental que nos permite conocer propiedades específicas de los polígonos regulares. Conocer cómo calcular la apotema de un hexágono y otros polígonos nos abre las puertas a un mundo de posibilidades en la resolución de problemas y comprensión de las figuras geométricas.

Cuáles son algunos consejos útiles para recordar y aplicar el cálculo de la apotema fácilmente

El cálculo de la apotema de un hexágono puede parecer complicado al principio, pero con los pasos correctos y algunos consejos útiles, puedes dominar fácilmente esta importante figura geométrica.

Paso 1: Conoce las propiedades del hexágono

Antes de calcular la apotema, es importante recordar las propiedades básicas de un hexágono. Un hexágono regular tiene seis lados iguales y seis ángulos internos de 120 grados cada uno. Esto nos brinda una base sólida para comenzar nuestro cálculo.

Paso 2: Encuentra el valor del lado del hexágono regular

La clave para calcular la apotema de un hexágono está en conocer el valor del lado del hexágono regular. Si no lo conoces, puedes utilizar alguna fórmula o medirlo directamente si tienes un hexágono físico a mano. Recuerda que todos los lados son iguales en un hexágono regular.

Paso 3: Divide el hexágono en triángulos equiláteros

Una vez que tienes el valor del lado del hexágono regular, puedes dividirlo en seis triángulos equiláteros. Esto se logra trazando tres diagonales que conectan los vértices del hexágono entre sí. Estos triángulos te permitirán trabajar con ángulos más manejables para el cálculo de la apotema.

Paso 4: Calcula el área de uno de los triángulos equiláteros

El siguiente paso es calcular el área de uno de los triángulos equiláteros. Puedes hacerlo utilizando la fórmula del área de un triángulo: Área = (base * altura) / 2. En este caso, la base es igual al lado del hexágono y la altura se calcula dividiendo este valor por 2√3.

Paso 5: Calcula el área total del hexágono regular

Luego de haber obtenido el área de uno de los triángulos equiláteros, debemos multiplicar ese valor por 6 para obtener el área total del hexágono regular. Esto se debe a que un hexágono está compuesto por seis triángulos equiláteros iguales.

Paso 6: Encuentra el valor del perímetro del hexágono regular

Ahora que sabemos el área total del hexágono regular, podemos encontrar el valor del perímetro utilizando la fórmula del área del hexágono regular: Perímetro = 6 * longitud del lado. Este resultado será útil en el siguiente paso.

Paso 7: Calcula la apotema del hexágono

Finalmente, podemos calcular la apotema utilizando la fórmula de la apotema de un polígono regular: Apotema = Área / (Perímetro / 2). Sustituyendo los valores que hemos obtenido hasta ahora, podemos encontrar el valor deseado.

Recuerda que practicar constantemente este cálculo te ayudará a dominarlo rápidamente. Además, puedes utilizar herramientas en línea o calculadoras para verificar tus resultados.

Dominar la geometría y el cálculo de la apotema de un hexágono es fundamental para resolver problemas más complejos en matemáticas y otras disciplinas. ¡Sigue estos pasos y estarás un paso más cerca de convertirte en un experto en geometría!

Preguntas frecuentes (FAQ)

1. ¿Qué es la apotema de un hexágono?

La apotema de un hexágono es la distancia desde el centro del hexágono hasta uno de sus lados.

2. ¿Cómo puedo calcular la apotema de un hexágono regular?

Para calcular la apotema de un hexágono regular, puedes utilizar la fórmula: apotema = lado * (√3 / 2).

3. ¿El valor de la apotema siempre es el mismo para todos los hexágonos regulares?

Sí, en un hexágono regular, la apotema siempre tendrá el mismo valor ya que todos sus lados y ángulos son iguales.

4. ¿Tengo que conocer el valor del lado para calcular la apotema?

Sí, necesitas conocer el valor del lado del hexágono para poder calcular la apotema utilizando la fórmula mencionada anteriormente.

5. ¿Cuál es la unidad de medida utilizada para la apotema de un hexágono?

La unidad de medida utilizada para la apotema de un hexágono puede variar según el sistema de medida utilizado, como centímetros, metros, pulgadas, etc.